【题目】用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是__(写出全等的简写).
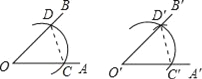
参考答案:
【答案】 SSS
【解析】本题考查了三角形全等的相关知识。
1、以O为圆心,任意长为半径用圆规画弧,分别交OA、OB于点C、D;
2、任意画一点O’,画射线O‘A‘,以O‘为圆心,OC长为半径画弧C‘E,交O‘A‘于点C‘;
3、以C‘为圆心,CD长为半径画弧,交弧C‘E于点D‘;
4、过点D‘画射线O‘B‘,∠A‘O‘B‘就是与∠AOB相等的角。
则通过作图我们可以得到OC=O′C′,OD=O′D′,CD=C′D′,从而可以利用SSS判定其全等。
OC=O′C′,OD=O′D′,CD=C′D′,从而可以利用SSS判定其全等。故填SSS.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个大的等腰三角形能被分割为两个小等腰三角形,则该大等腰三角形顶角的度数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正
 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?

-
科目: 来源: 题型:
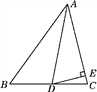
查看答案和解析>>【题目】在△ABC中,AD是角平分线,∠B=54°,∠C=76°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC,求∠EDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂接到一批服装加工业务,若由甲车间独做,可比规定时间提前8天完成,甲车间在制作完这批服装的60%后因另有任务,立即将剩余服装全部交给乙车间,结果刚好按规定时间完成.已知甲、乙两个车间每天分别制作200和120件服装,求该工厂所接的这批服装的件数和规定时间.
-
科目: 来源: 题型:
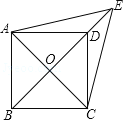
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
相关试题

