【题目】某水果店第一次用600元购进水果若干千克,第二次又用600元购进该水果,但这次每千克的进价比第一次进价的提高了25%,购进数量比第一次少了30千克.
(1)求第一次每千克水果的进价是多少元?
(2)若要求这两次购进的水果按同一价格全部销售完毕后获利不低于420元,问每千克售价至少是多少元?
参考答案:
【答案】
(1)解:设第一次每千克水果是进价为x元,
根据题意列方程得, ![]() ﹣
﹣ ![]() =30,
=30,
解得x=4,
经检验:x=4是原分式方程的解.
答:第一次每千克水果的进价为4元
(2)解:设售价为y元,第一次每千克水果的进价为4元,则第二次每千克水果的进价为4×(1+25%)=5(元)
根据题意列不等式为:![]() ×(y﹣4)+
×(y﹣4)+ ![]() ×(y﹣5)≥420,
×(y﹣5)≥420,
解得y≥6.
答:每千克水果售价至少是6元.
【解析】(1)用x的代数式分别表示第一二次的数量,“数量比第一次少了30千克”可列分式方程,求出x;(2)由“获利不低于420元”可列不等式,求出售价的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
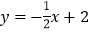 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
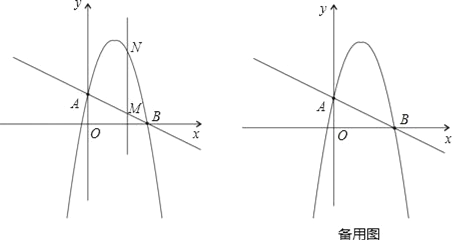
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球,小明和小东同时从袋中随机各摸出1个球,并计算这两球上的数字之和,当和小于9时小明获胜,反之小东获胜.
(1)请用树状图或列表的方法,求小明获胜的概率;
(2)这个游戏公平吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(3,﹣2)关于y轴对称的点的坐标是( )
A. (3,2) B. (3,﹣2) C. (﹣3,2) D. (﹣3,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在梯形ABCD中,AD∥BC,且AD=4cm,AB=6cm,BC=12cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动. 当Q点到达B点时,动点P、Q同时停止运动. 设点P、Q同时出发,并运动了t秒.
(1)求梯形ABCD的面积.
(2)当t为何值时,四边形PQCD成为平行四边形?
(3)是否存在t,使得P点在线段DC上,且PQ⊥DC(如图(2)所示)?若存在,求出此时t的值,若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式3x﹣2>4的解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算﹣4×(﹣2)的结果是( )
A.8
B.﹣8
C.6
D.﹣2
相关试题

