【题目】“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
参考答案:
【答案】解:(1)设“益安”车队载重量为8吨、10吨的卡车分别有x辆、y辆,
根据题意得: ![]() ,解得:
,解得: ![]() 。
。
答:“益安”车队载重量为8吨的卡车有5辆,10吨的卡车有7辆。
(2)设载重量为8吨的卡车增加了z辆,
依题意得:8(5+z)+10(7+6﹣z)>165,解得:z<![]() 。
。
∵z≥0且为整数,∴z=0,1,2,6﹣z=6,5,4。
∴车队共有3种购车方案:
①载重量为8吨的卡车不购买,10吨的卡车购买6辆;
②载重量为8吨的卡车购买1辆,10吨的卡车购买5辆;
③载重量为8吨的卡车购买2辆,10吨的卡车购买4辆。
【解析】试题分析:(1)根据“车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石”分别得出等式组成方程组,求出即可;
(2)利用“车队需要一次运输沙石165吨以上”得出不等式,求出购买方案即可.
试题解析:(1)设该车队载重量为8吨、10吨的卡车分别有x辆、y辆,
根据题意得: ![]() ,
,
解之得: ![]() .
.
答:该车队载重量为8吨的卡车有5辆,10吨的卡车有7辆;
(2)设载重量为8吨的卡车增加了z辆,
依题意得:8(5+z)+10(7+6z)>165,
解之得: ![]() ,
,
∵![]() 且为整数,
且为整数,
∴z=0,1,2;
∴6z=6,5,4.
∴车队共有3种购车方案:
①载重量为8吨的卡车购买1辆,10吨的卡车购买5辆;
②载重量为8吨的卡车购买2辆,10吨的卡车购买4辆;
③载重量为8吨的卡车不购买,10吨的卡车购买6辆
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
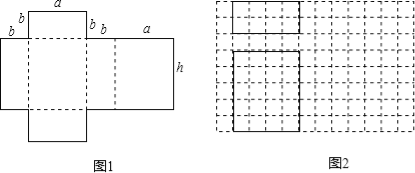
(1)这个几何体模型的名称是 .
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足
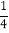 a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(﹣m,n),B(0,m),且m、n满足
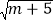 +(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
(1)写出D点坐标并求A、D两点间的距离;
(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;
(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围.
-
科目: 来源: 题型:
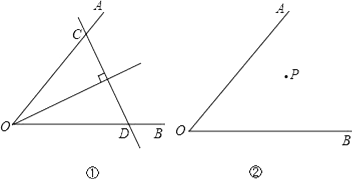
查看答案和解析>>【题目】已知∠AOB及其内部一点P,试讨论以下问题的解答:
(1)如图①,若点P在∠AOB的平分线上,我们可以过P点作直线垂直于角平分线,分别交OA、OB于点C、D,则可以得到△OCD是以CD为底边的等腰三角形;若点P不在∠AOB的平分线上(如图②),你能过P点作直线,分别交OA、OB于点C、D,得到△OCD是等腰三角形,且CD是底边吗?请你在图②中画出图形,并简要说明画法.
(2)若点P不在∠AOB的平分线上(如图③),我们可以过P点作PQ∥OA,并作∠QPR=∠AOB,直线PR分别交OA、OB于点C、D,则可以得到△OCD是以OC为底的等腰三角形.请你说明这样作的理由.
(3)若点P不在∠AOB的平分线上,请你利用在(2)中学到的方法,在图④中过P点作直线分别交OA、OB于点C、D,使得△OCD是等腰三角形,且OD是底边.保留画图的痕迹,不用写出画法.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,现计划用210000元资金,购买这三种树共1000棵.
(1)求乙、丙两种树每棵各多少元?
(2)若购买甲种树的棵树是乙种树的2倍,恰好用完计划资金,求这三种树各能购买多少棵?
(3)若又增加了10120元的购树款,在购买总棵树不变的前提下,求丙种树最多可以购买多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+y)2=7,(x﹣y)2=3,则xy的值为( )
A.2B.1C.﹣1D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a>8),就站在A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人.
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少?(用含a的代数式表示)
(2)此时,若小杰迅速从A窗口队伍转移到B窗口后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围.(不考虑其它因素)
相关试题

