【题目】已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
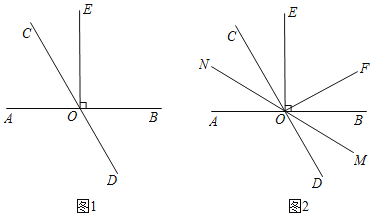
(1)如图1,∠BOC=2∠AOC,求∠COE的度数;
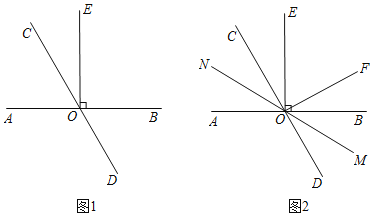
(2)如图2.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与2∠EOF度数相等的角.
参考答案:
【答案】(1)∠COE=30°;(2)与2∠EOF度数相等的角是:∠AOD,∠BOC,∠FON,∠EOM.
【解析】
(1)先根据平角的定义可得∠AOC=60![]() ,再利用垂直的定义可得∠AOE=90
,再利用垂直的定义可得∠AOE=90![]() ,从而得结论;
,从而得结论;
(2)根据(1)中∠AOC=60![]() ,分别计算各角的度数,得其中∠EOF=60
,分别计算各角的度数,得其中∠EOF=60![]() ,根据各角的度数可得结论.
,根据各角的度数可得结论.
(1)如图1,∵∠AOC+∠BOC=180![]() ,且∠BOC=2∠AOC,
,且∠BOC=2∠AOC,
∴∠AOC=60![]() ,
,
∵OE⊥AB,
∴∠AOE=90![]() ,
,
∴∠COE=90![]() ﹣60
﹣60![]() =30
=30![]() ;
;
(2)如图2,由(1)知:∠AOC=60![]() ,
,
∵射线OM平分∠BOD,
∴∠BOM=∠DOM=∠AON=∠CON=30![]() ,
,
∵OE⊥AB,OC⊥OF,
∴∠AOE=∠COF=90![]() ,
,
∴∠AOC=∠EOF=60![]() ,
,
∴∠AOD=∠BOC=∠FON=∠EOM=180![]() ﹣60
﹣60![]() =120
=120![]() =2∠EOF,
=2∠EOF,
∴与2∠EOF度数相等的角是:∠AOD,∠BOC,∠FON,∠EOM.
-
科目: 来源: 题型:
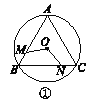
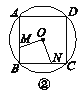
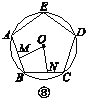
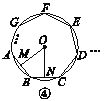
查看答案和解析>>【题目】如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
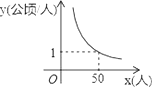
A. 该村人均耕地面积随总人口的增多而增多
B. 该村人均耕地面积y与总人口x成正比例
C. 若该村人均耕地面积为2公顷,则总人口有100人
D. 当该村总人口为50人时,人均耕地面积为1公顷
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:

(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
-
科目: 来源: 题型:
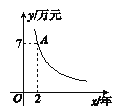
查看答案和解析>>【题目】朱先生利用分期付款的形式购买了一套住房,他购买的住房的价格为24万元,交了首付之后每年付款y万元,x年结清余款,y与x的函数关系如图所示,请根据图象所提供的信息,回答下列问题:
(1)确定y与x的函数解析式,并求出首付款的数目;
(2)朱先生若用10年结清余款,则每年应付多少钱?
(3)如果朱先生打算每年付款不超过7000元,那么他至少需要几年才能结清余款?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线AB与直线PQ交于点E,直线CD与直线PQ交于点F,∠PEB+∠QFD=180°.
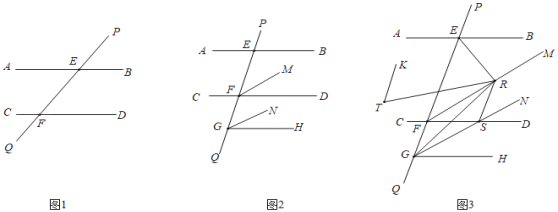
(1)如图1,求证:AB∥CD;
(2)如图2,点G为直线PQ上一点,过点G作射线GH∥AB,在∠EFD内过点F作射线FM,∠FGH内过点G作射线GN,∠MFD=∠NGH,求证:FM∥GN;
(3)如图3,在(2)的条件下,点R为射线FM上一点,点S为射线GN上一点,分别连接RG、RS、RE,射线RT平分∠ERS,∠SGR=∠SRG,TK∥RG,若∠KTR+∠ERF=108°,∠ERT=2∠TRF,∠BER=40°,求∠NGH的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )

A.50B.62C.65D.68
相关试题

