【题目】已知，抛物线y=ax2+bx+c（a≠0）的顶点为A（s，t）（其中s≠0）．

（1）若抛物线经过（2，7）和（-3，37）两点，且s=1．

①求抛物线的解析式；

②若n＞1，设点M（n，y1），N（n+1，y2）在抛物线上，比较y1，y2的大小关系，并说明理由；

（2）若a=2，c=-2，直线y=2x+m与抛物线y=ax2+bx+c的交于点P和点Q，点P的横坐标为h，点Q的横坐标为h+3，求出b和h的函数关系式；

（3）若点A在抛物线y=上，且2≤s＜3时，求a的取值范围．

【答案】（1）①；②，理由见解析；（2）；（3）

【解析】

（1）①已知抛物线上的两点，以及顶点的横坐标，列出方程组，即可求解；

②由①知抛物线开口向上，以及抛物线的对称轴，且点M、N均在对称轴的右侧，根据抛物线的性质，在对称轴的右侧随着的增大而增大，即可比较，的大小；

（2）根据点、既在抛物线上，又在直线上，分别代入，表示出坐标，根据纵坐标差值相等，即可求得和的函数关系式；

（3）抛物线经过点（， ），将其代入，可求得，点A在，也可表示出，通过代换，可求得关于的表达式，根据2≤s＜3，解不等式组即可求解．

解（1）①∵抛物线经过点（2，7）和（-3，37）两点，且顶点为A（s，t），

则有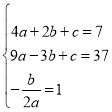： ，解得： ，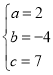

故抛物线的解析式为：；

②由①知：抛物线的对称轴为，且开口向上，

∴抛物线在的右侧随着的增大而增大，

而n＞1，点M（n，y1），N（n+1，y2）均在对称轴的右侧，且，

∴；

（2）若a=2，c=-2，则抛物线为：，点、在抛物线上，

则（， ），（，），

同时点、也在直线上，则（，），（，），

而无论点、在抛物线上还是在直线上，它们纵坐标的差值是相等的，故有：

=，

整理得：；

故b和h的函数关系式为；

（3）设抛物线，

∵抛物线经过点（，），

∴ ，即，①

又∵点A 在抛物线，则 ，即，②

由①②可得：，且，

∴，

∵，即，

解得：．

故当2≤s＜3时，a的取值范围．

关闭