【题目】在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 且相交于点
且相交于点![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 与直线
与直线![]() ,
,![]() 分别相交于点
分别相交于点![]() 、
、![]() ,点
,点![]() 是线段
是线段![]() 的中点,以点
的中点,以点![]() 为顶点的抛物线
为顶点的抛物线![]() 经过点
经过点![]() .
.
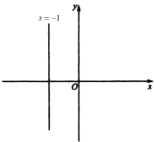
(1)①点![]() 的坐标是________;
的坐标是________;
②点![]() 的坐标是________.(用含
的坐标是________.(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)求![]() 的值(用含
的值(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)若![]() ,当
,当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
【解析】
(1)①由![]() 与x轴交于点B求得;
与x轴交于点B求得;
②根据直线![]() 与直线
与直线![]() ,
,![]() 分别相交于点
分别相交于点![]() 、
、![]() ,分别求出点C、D的坐标,利用点
,分别求出点C、D的坐标,利用点![]() 是线段
是线段![]() 的中点利用中点公式求出点P的纵坐标即可;
的中点利用中点公式求出点P的纵坐标即可;
(2)根据点P是抛物线的顶点设抛物线的解析式为![]() ,解方程组
,解方程组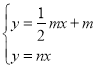 求出点A的坐标,再将点A的坐标代入抛物线的解析式即可求出a;
求出点A的坐标,再将点A的坐标代入抛物线的解析式即可求出a;
(3)由![]() 求出
求出![]() ,得到点
,得到点![]() 的坐标为
的坐标为![]() ,再分
,再分![]() 、
、![]() 两种情况分别求出m的取值范围.
两种情况分别求出m的取值范围.
(1)①∵![]() 与x轴交于点B,
与x轴交于点B,
∴当y=0时,得x=-2,
∴点B的坐标是(-2,0),
故答案为:![]() .
.
②∵直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,
∴当x=-1时,![]() =
=![]() ,
,
∴C(-1,![]() ),
),
∵直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,
∴当x=-1时,y=nx=-n,
∴D(-1,-n),
∴CD∥y轴,
∴点P的横坐标是-1,纵坐标是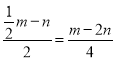 ,
,
故答案为:![]() .
.
(2)设抛物线的解析式为![]() .
.
![]() 直线
直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,
,
∴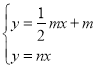 ,解得
,解得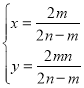 .
.
![]() 点
点![]() 的坐标是
的坐标是![]() .
.
![]() .
.
解得![]() .
.
(3)当![]() 时,
时,![]() .
.
![]() 抛物线解析式可以转化为
抛物线解析式可以转化为![]() .
.
![]() 点
点![]() 的坐标可以表示为
的坐标可以表示为![]() .
.
当![]() 时,抛物线开口向下,
时,抛物线开口向下,
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
![]() .解得
.解得![]() .
.
![]() .即
.即![]()
解得![]() .
.
当![]() 时,抛物线开口向上,
时,抛物线开口向上,
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
![]() .解得
.解得![]() .
.
![]() .即
.即![]() .
.
解得![]() .
.
综上,![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.

