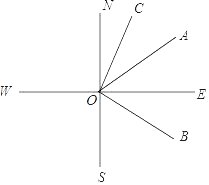
【题目】如图,直线SN⊥直线WE,垂足是点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)写出图中与∠BOE互余的角: .
(2)若射线OA是∠BON的角平分线,探索∠BOS与∠AOC的数量关系.
参考答案:
【答案】(1)∠BOS,∠COE;(2)∠AOC=![]() ∠BOS.
∠BOS.
【解析】
(1)由图直接可知与∠BOE互余的角为∠BOS,∠BOS+∠CON+∠BOE+COE=180°,再由m°的角与n°的角互余可得∠BOE+∠COE=90°,据此可进行解答;
(2)由射线OA是∠BON的角平分线可得∠NOA=![]() ∠NOB,再由∠BOS与∠BON互补可求得∠NOA=
∠NOB,再由∠BOS与∠BON互补可求得∠NOA=![]() ∠BON=
∠BON=![]() (180°﹣∠BOS)=90°﹣
(180°﹣∠BOS)=90°﹣![]() ∠BOS;由∠NOC与∠BOS互余可得∠AOC=∠NOA﹣∠NOC=90°﹣
∠BOS;由∠NOC与∠BOS互余可得∠AOC=∠NOA﹣∠NOC=90°﹣![]() ∠BOS﹣(90°﹣∠BOS)=
∠BOS﹣(90°﹣∠BOS)=![]() ∠BOS.
∠BOS.
解:(1)首先与∠BOE互余的角有∠BOS,
由m°的角与n°的角互余知∠BOS+∠CON=90°,
∵∠BOS+∠CON+∠BOE+COE=180°,
∴∠BOE+∠COE=90°,
与∠BOE互余的角有∠BOS,∠COE,
故答案为:∠BOS,∠COE;
(2)∠AOC=![]() ∠BOS.
∠BOS.
∵射线OA是∠BON的角平分线,
∴∠NOA=![]() ∠NOB,
∠NOB,
∵∠BOS+∠BON=180°,
∴∠BON=180°﹣∠BOS,
∠NOA=![]() ∠BON=90°﹣
∠BON=90°﹣![]() ∠BOS,
∠BOS,
∵∠NOC+∠BOS=90°,∠NOC=90°﹣∠BOS,
∴∠AOC=∠NOA﹣∠NOC=90°﹣![]() ∠BOS﹣(90°﹣∠BOS)=
∠BOS﹣(90°﹣∠BOS)=![]() ∠BOS
∠BOS
∴∠AOC=![]() ∠BOS.
∠BOS.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形AOCB的边长为4,反比例函数y=
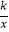 (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 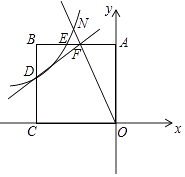
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= 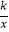 (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=﹣
 (x﹣2)2﹣3,下列说法错误的是( )
(x﹣2)2﹣3,下列说法错误的是( )
A.图象的开口向下
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(2,﹣3)
D.图象与y轴的交点坐标为(0,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是( )
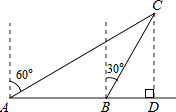
A.20海里
B.40海里
C.20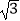 海里
海里
D.40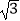 海里
海里 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( )
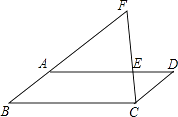
A.EF=2CE
B.S△AEF= S△BCF
S△BCF
C.BF=3CD
D.BC= AE
AE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是 .
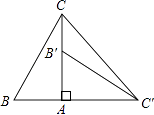
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
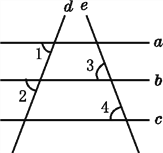
解:a与c平行.
理由:因为∠1=∠2(_________________),
所以a∥b(_________________).
因为∠3=∠4(_________________),
所以b∥c(_________________).
所以a∥c(_________________).
相关试题

