【题目】问题情景:如图1,![]() 中,有一块直角三角板
中,有一块直角三角板![]() 放置在
放置在![]() 上(
上(![]() 点在
点在![]() 内),使三角板
内),使三角板![]() 的两条直角边
的两条直角边![]() 、
、![]() 恰好分别经过点
恰好分别经过点![]() 和点
和点![]() .
.
试问![]() 与
与![]() 是否存在某种确定的数量关系?
是否存在某种确定的数量关系?
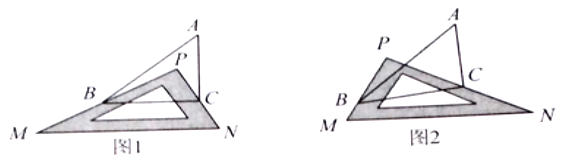
(1)特殊研究:若![]() ,则
,则![]() 度,
度,![]() 度,
度,![]() 度;
度;
(2)类比探索:请探究![]() 与
与![]() 的关系.
的关系.
(3)类比延伸:如图2,改变直角三角包![]() 的位置;使
的位置;使![]() 点在
点在![]() 外,三角板
外,三角板![]() 的两条直角边
的两条直角边![]() 、
、![]() 仍然分别经过点
仍然分别经过点![]() 和点
和点![]() ,(2)中的结论是否仍然成立?若不成立请直接写出你的结论.
,(2)中的结论是否仍然成立?若不成立请直接写出你的结论.
参考答案:
【答案】(1)140,90,50;(2)结论:∠ABP+∠ACP=90°﹣∠A,理由详见解析;(3)不成立,存在结论:∠ACP﹣∠ABP=90°﹣∠A.
【解析】
(1)已知![]() ,根据三角形的内角和定理求出
,根据三角形的内角和定理求出![]() 的度数,已知∠P=90°,根据三角形的内角和定理求出
的度数,已知∠P=90°,根据三角形的内角和定理求出![]() 的度数,进而得到
的度数,进而得到![]() 的度数;
的度数;
(2)由(1)中![]() 的度数,
的度数,![]() 的度数,相减即可得到
的度数,相减即可得到![]() 与∠A的关系;
与∠A的关系;
(3)在△ABC中,![]() =180°-∠A,同理在△PBC中,
=180°-∠A,同理在△PBC中,![]() =90°,相减可得到∠ACP﹣∠ABP=90°﹣∠A.
=90°,相减可得到∠ACP﹣∠ABP=90°﹣∠A.
解:(1)∵![]()
∴![]() =180°-∠A=140°,
=180°-∠A=140°,
∵∠P=90°,
∴![]() =90°,
=90°,
∴![]() =140°-90°=50°,
=140°-90°=50°,
(2)结论:∠ABP+∠ACP=90°﹣∠A.
证明:∵90°+(∠ABP+∠ACP)+∠A=180°,
∴∠ABP+∠ACP+∠A=90°,
∴∠ABP+∠ACP=90°﹣∠A.
(3)不成立;存在结论:∠ACP﹣∠ABP=90°﹣∠A.
理由:在△ABC中,![]() =180°-∠A,
=180°-∠A,
在△PBC中,∠P=90°,∴![]() =90°,
=90°,
∴(![]() )-(
)-(![]() )=180°-∠A-90°,
)=180°-∠A-90°,
即![]() =90°﹣∠A.
=90°﹣∠A.
∴∠ACP﹣∠ABP=90°﹣∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形
 内,若两张边长分别为
内,若两张边长分别为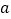 和
和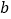 (
( )的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形总未被这两张正方形纸片覆盖的部分用阴影表示,若图1中阴影部分的面积为
)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形总未被这两张正方形纸片覆盖的部分用阴影表示,若图1中阴影部分的面积为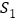 ,图2中阴影部分的面积和为
,图2中阴影部分的面积和为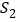 ,则关于
,则关于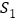 ,
,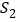 的大小关系表述正确的是( )
的大小关系表述正确的是( )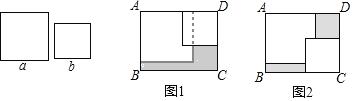
A.
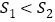 B.
B.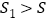 C.
C.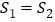 D.无法确定
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
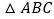 中,
中,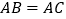 ,高
,高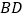 、
、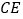 相交于点
相交于点 ,连接
,连接 并延长交
并延长交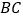 于点
于点 ,则图中全等的直角三角形共有( )
,则图中全等的直角三角形共有( )
A.4对B.5对C.
 对D.7对
对D.7对 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数

100
200
300
500
800
1000
3000
摸到白球的次数

65
124
278
302
481
599
1803
摸到白球的频率

0.65
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计当
 很大时,摸到白球的频率将会接近 (精确到0.1);
很大时,摸到白球的频率将会接近 (精确到0.1);(2)假如摸一次,摸到黑球的概率
 ;
;(3)试估算盒子里黑颜色的球有多少只.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,﹣4),B(5,﹣4),C(4,﹣1).
(1)将△ABC经过平移得到△A1B1C1,若点C的应点C1的坐标为(2,5),则点A,B的对应点A1,B1的坐标分别为 ;
(2)在如图的坐标系中画出△A1B1C1,并画出与△A1B1C1关于原点O成中心对称的△A2B2C2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)如图,EF//AD,
 =
= .求证:∠DGA+∠BAC=180°.请将说明过程填写完成.
.求证:∠DGA+∠BAC=180°.请将说明过程填写完成.
证明:∵EF//AD,(已知)
∴
 =_____(_____________________________).
=_____(_____________________________).又∵
 =
= (______)
(______)∴
 =
= (________________________).
(________________________).∴AB//______(____________________________)
∴∠DGA+∠BAC=180°(_____________________________)
-
科目: 来源: 题型:
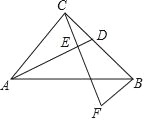
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.
求证:AC=2BF.
相关试题

