【题目】已知：点为图形上任意一点，点为图形上任意一点，若点与点之间的距离始终满足，则称图形与图形相离．

（1）已知点、、、．

①与直线相离的点是 ；

②若直线与相离，求的取值范围；

（2）设直线、直线及直线围成的图形为，⊙的半径为，圆心的坐标为，直接写出⊙与图形相离的的取值范围．

【答案】（1）①A、C；②b的取值范围是b>﹣1或b<﹣7；（2）t的取值范围是：t＜或t＞或＜t＜．

【解析】

（1）①将A，B，C，D四个点的坐标依次代入直线解析式，不在直线上的点即为符合题意的点；

②当直线y＝3x+b经过点A和点C时计算b的值，进而可得答案；

（2）分三种情形：如图1，当⊙T位于直线AC右侧，且与直线AC相切于点H，利用解直角三角形的知识求出TD，进而可得点T的坐标，从而可得t的取值范围；如图2，当⊙T位于直线左侧，且与直线AB相切于点H，同理求出点T的坐标即得t的取值范围；③如图3，分⊙T位于直线AC左侧，且与直线AC相切、⊙T与AB相切，且位于直线AB的右侧时两种情况，分别求出点T的坐标即得t的取值范围，从而可得结果．

解：（1）①∵点A（1，2），

∴当x＝1时，3﹣5＝﹣2，

∴点A不在直线y＝3x﹣5上，

同理，点C（2，﹣1）不在直线y＝3x﹣5上，点B（0，﹣5），点D（3，4）在直线上，

∴与直线y＝3x﹣5相离的点是A，C；

故答案为：A，C；

②当直线y＝3x+b过点A（1，2）时，则3+b＝2，∴b＝﹣1．

当直线y＝3x+b过点C（2，﹣1）时，则6+b＝﹣1，∴b＝﹣7．

∴b的取值范围是b＞﹣1或b＜﹣7；

（2）①如图1，图形W为△ABC，直线与y轴交于点A，与x轴交于点D，

令x＝0，y＝3，令y＝0，x＝，

∴OA＝3，OD＝，

∴∠OAD＝30°，∠ADO＝60°，

当⊙T位于直线AC右侧，且与直线AC相切于点H，连接TH，则TH⊥DH，

∵∠TDH＝∠ADO＝60°，TH＝1，

∴DT＝，

∴OT＝OD+DT＝，∴T（，0），

∴当t＞时，⊙T与图形W相离；

②如图2，当⊙T位于直线左侧，且与直线AB相切于点H，连接TH，直线AB与x轴交于点E，

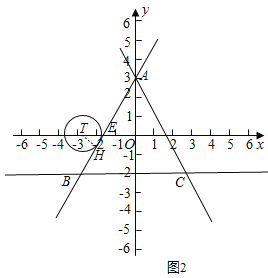
同理可得，TE＝，OE＝，

∴OT＝，∴T（﹣，0），

∴当t＜﹣时，⊙T与图形W相离；

③如图3，当⊙T位于直线AC左侧，且与直线AC相切时，

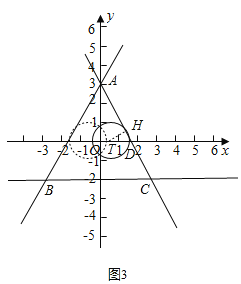
同理可得TD＝，OD＝，

∴OT＝OD﹣TD＝，∴T（，0），

当⊙T与AB相切，且位于直线AB的右侧时，同理可得T（﹣，0），

∴当﹣＜t＜时，⊙T与图形W相离．

综上：⊙与图形相离时，t的取值范围是：t＜或t＞或＜t＜．

关闭