【题目】学校组织植树活动,已知在甲处植树的有14人,在乙处植树的有6人,现调70人去支援.
(1)若要使在甲处植树的人数与在乙处植树的人数相等,应调往甲处 人.
(2)若要使在甲处植树的人数是在乙处植树人数的2倍,问应调往甲、乙两处各多少人?
(3)通过适当的调配支援人数,使在甲处植树的人数恰好是在乙处植树人数的n倍(n是大于1的正整数,不包括1.)则符合条件的n的值共有 个.
参考答案:
【答案】(1)31;(2)应调往甲处46人,乙处24人.(3)6.
【解析】
试题分析:(1)设调往甲处y人,则调往乙处(70﹣y)人,由题意得等量关系:在甲处植树的人数=在乙处植树的人数,根据等量关系列出方程,再解即可;
(2)设调往甲处x人,则调往乙处(70﹣x)人,由题意得等量关系:在甲处植树的人数=在乙处植树的人数×2,根据等量关系列出方程,再解即可;
(3)设调往甲处z人,则调往乙处(70﹣z)人,由题意得等量关系:在甲处植树的人数=在乙处植树的人数×n,根据等量关系列出方程,再求出整数解即可.
解:(1)设调往甲处y人,则调往乙处(70﹣y)人,由题意得:
14+y=6+(70﹣y),
解得:y=31,
故答案为:31;
(2)解:设调往甲处x人,则调往乙处(70﹣x)人,由题意得:
14+x=2(6+70﹣x),
解得:x=46
成人数:70﹣46=24(人),
答:应调往甲处46人,乙处24人.
(3)设调往甲处z人,则调往乙处(70﹣z)人,列方程得
14+z=n(6+70﹣z),
14+z=n(76﹣z),
n=![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
共6种,
故答案为:6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长分别为5cm和10 cm,则此三角形的周长是( )
A. 15 cm B. 20 cm C. 25 cm D. 20 cm或25 cm
-
科目: 来源: 题型:
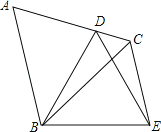
查看答案和解析>>【题目】如图,△ABC是等边三角形,点D为AC边上一点,以BD为边作等边△BDE,连接CE.若CD=1,CE=3,则BC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为 cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两数之和为负,积为正,则这两个数应是
A、同为负数 B、同为正数 C、一正一负 D、有一个为0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=mx2﹣(m+1)x+1.
(1)求证:该抛物线与x轴总有交点;
(2)若m为整数,当一元二次方程mx2﹣(m+1)x+1=0的根都是整数时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段长为边,能组成三角形的是( )
A. 1 cm,2 cm,4 cm B. 8 cm,6 cm,4 cm
C. 12 cm,5 cm,6 cm D. 2 cm,3 cm ,5 cm
相关试题

