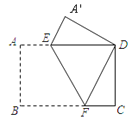
【题目】把一张矩形纸片ABCD按如图方式折叠，使顶点B和D重合，点A到点A’，折痕为EF．

(1)连接BE，求证：四边形BFDE是菱形；

(2)若AB＝8cm，BC＝16cm，求线段DF的长．

参考答案：

【答案】（1）证明见解析；（2）10.

【解析】（1）利用翻折变换的性质得出∠2=∠3，BE=DE，BF=DF，进而利用等腰三角形的性质得出三条边相等即可；

（2）利用勾股定理得出AE的长，进而得出DE的长，再利用三角形面积公式求出即可．

解：（1）证明：由折叠的性质可得∠BFE=∠DEF，

∵AD∥BC，

∴∠BFE=∠DEF，

∴∠DFE=∠DEF，

∴DE=DF，

∴四边形BFDE是平行四边形，

由折叠知，BF=DF，

∴四边形EBFD是菱形；

（2）解： 在Rt△ABE中，设DF=x，则BF= x，CF=16-x，

由勾股定理得：

∴x2=（16-x）2+82，

解得：x=10，

∴线段DF的长为10．

“点睛”此题主要考查了翻折变换的性质以及勾股定理和菱形的判定等知识，解题关键是用方程思想求出线段DF的长．

关闭