【题目】在△ABC中,AB=AC=4,∠BAC=30°,以AC为一边作等边△ACD,连接BD.请画出图形,并直接写出△BCD的面积.
参考答案:
【答案】4![]() -4.
-4.
【解析】试题分析:首先根据题意画出图形,然后把BC边上的高作出来,过点D作DE⊥BC交BC的延长线于点E,利用勾股定理以及锐角三角函数求出BC,DE的长,进而求出△BCD的面积.
试题解析:首先根据题意画出图形,如图,由题意可知AB=AC=4,∠BAC=30°,△ACD是等边三角形,则AB=AD=DC=AC=4,∠BAD=∠BAC+∠CAD=30°+60°=90°,∠ABC=∠ACB=(180°-30°)÷2=75°,∴△ABD是等腰直角三角形,∴∠ABD=∠ADB=45°,∠DBE=75°-45°=30°,∠DCE=180°-60°-75°=45°,则△DCE是等腰直角三角形,CE=DE,∵DC=4,∴DE=EC=![]() =
=![]() ,∴BD=2DE=
,∴BD=2DE=![]() ,∴BE=BDcos30°=
,∴BE=BDcos30°=![]() ×
×![]() =
=![]() ,∴BC=BE﹣EC=2
,∴BC=BE﹣EC=2![]() ﹣2
﹣2![]() ,∴△BCD的面积为:
,∴△BCD的面积为: ![]() ×2
×2![]() ×(2
×(2![]() ﹣2
﹣2![]() )=4
)=4![]() ﹣4.
﹣4.

-
科目: 来源: 题型:
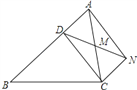
查看答案和解析>>【题目】已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:AD=CN;
②若∠BAN=90度,求证:四边形ADCN是矩形.
-
科目: 来源: 题型:
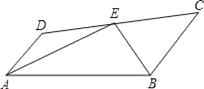
查看答案和解析>>【题目】如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x﹣3)2+|y﹣4|=0.
(1)求AD和BC的长;
(2)你认为AD和BC还有什么关系?并验证你的结论;
(3)你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽在超市买一食品,外包装上印有“总净含量(200±5)g”的字样.小明拿去称了一下,发现只有197g.则食品生产厂家___________(填“有”或“没有”)欺诈行为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式:①45;②(-3)20;③0100;④(-1)100;⑤(-1)305;⑥-62.其中,运算结果为正数的有________,运算结果为负数的有________,运算结果为0的有________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. (-2×3)2=-36
B. 32×(-32)=0
C. -24=-16
D. 23=32
相关试题

