Question

【题目】阅读下列材料，然后解答问题．

经过正四边形(即正方形)各顶点的圆叫做这个正四边形的外接圆，圆心是正四边形的对称中心，这个正四边形叫做这个圆的内接正四边形．

如图，正方形ABCD内接于⊙O，⊙O的面积为S1，正方形ABCD的面积为S2．以圆心O为顶点作∠MON，使∠MON＝90°．将∠MON绕点O旋转，OM、ON分别与⊙O交于点E、F，分别与正方形ABCD的边交于点G、H．设由OE、OF、及正方形ABCD的边围成的图形(阴影部分)的面积为S．

（1）当OM经过点A时(如图①)，则S、S1、S2之间的关系为： (用含S1、S2的代数式表示)；

（2）当OM⊥AB于G时(如图②)，则(1)中的结论仍然成立吗？请说明理由；

（3）当∠MON旋转到任意位置时（如图③），则（1）中的结论任然成立吗：请说明理由.

Answer 1

【答案】（1）；

（2）（1）中的结论仍然成立，理由见解析；

（2）（1）中的结论仍然成立，理由见解析.

【解析】试题分析：（1）结合正方形的性质及等腰直角三角形的性质，容易得出结论；

（2）仍然成立，可证得四边形OGHB为正方形，则可求出阴影部分的面积为扇形OEF的面积减去正方形OGBH的面积；

（3）仍然成立，过O作OR⊥AB，OS⊥BC，垂足分别为R、S，则可证明△ORG≌△OSH，可得出四边形ORBS的面积=四边形OGBH的面积，再利用扇形OEF的面积减正方形ORBS的面积即可得出结论．

试题解析：（1）当OM经过点A时由正方形的性质可知：∠MON=90°，

∴S△OAB=S正方形ABCD=S2，S扇形OEF=S圆O=S1，

∴S=S扇形OEF-S△OAB=S圆O-S正方形ABCD=S1-S2=（S1-S2），

（2）结论仍然成立，理由如下：

∵∠EOF=90°，

∴S扇形OEF=S圆O=S1

∵∠OGB=∠EOF=∠ABC=90°，

∴四边形OGBH为矩形，

∵OM⊥AB，

∴BG=AB=BC=BH，

∴四边形OGBH为正方形，

∴S四边形OGBH=BG2=（AB）2=S2，

∴S=S扇形OEF-S四边形OGBH=S1-S2=（S1-S2）；

（3）（1）中的结论仍然成立，理由如下：

∵∠EOF=90°，

∴S扇形OEF=S圆O=，

过O作OR⊥AB，OS⊥BC，垂足分别为R、S，

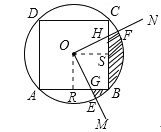
由（2）可知四边形ORBS为正方形，

∴OR=OS，

∵∠ROS=90°，∠MON=90°，

∴∠ROG=∠SOH=90°-∠GOS，

在△ROG和△SOH中，

，

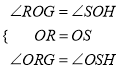∴△ROG≌△SOH（ASA），

∴S△ORG=S△OSH，

∴S四边形OGBH=S正方形ORBS，

由（2）可知S正方形ORBS=S2，

∴S四边形OGBH=S2，

∴S=S扇形OEF-S四边形OGBH=（S1-S2）．