【题目】去年暑假,某旅行社组织了一个中学生“夏令营”活动,共有253名中学生报名参加,打算选租甲、乙两种客车载客到指定地点.甲客车2辆、乙客车1辆可坐110人,甲客车3辆、乙客车2辆可坐180人.旅行前,旅行社每辆车安排了一名带队老师,因此一共安排了7名带队老师.
(1)甲、乙两种客车各可坐多少人?
(2)请帮助旅行社设计租车方案.
参考答案:
【答案】(1)甲、乙两种客车分别可坐40人、30人;(2)有三种租车方案:租甲种客车5辆,租乙种客车2辆;租甲种客车6辆,租乙种客车1辆,租甲种客车7辆,租乙种客车0辆.
【解析】
(1)设甲、乙两种客车可分别坐x人,y人,利用甲客车2辆、乙客车1辆可坐110人;甲客车3辆、乙客车2辆可坐180人列两个方程组成方程组,然后解方程组即可;
(2)设租甲种客车a辆,则租乙种客车(7-a)辆,利用乘车人数不少于253+7列不等式得到40a+30(7-a)≥253+7,再解不等式得到a≥5,加上a≤7,于是可得到a=5、6、7,然后写出三个方案.
(1)设甲、乙两种客车可分别坐x人,y人,
根据题意,得![]() ,
,
解得![]() ,
,
答:甲、乙两种客车分别可坐40人、30人;
(2)设租甲种客车a辆,则租乙种客车(7-a)辆,
根据题意得40a+30(7-a)≥253+7,
解得a≥5,
所以5≤a≤7,
而a为整数,
所以a=5、6、7,
有三种租车方案:租甲种客车5辆,租乙种客车2辆;租甲种客车6辆,租乙种客车1辆,租甲种客车7辆,租乙种客车0辆,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有小正方形的边长都为1,A、B、C都在格点上.
(1)过点C画直线AB的平行线(不写画法,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段_____的长度是点A到直线BC的距离;
(4)线段AG、AH的大小关系为AG_____AH.(填“>”或“<”或“=”),理由________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A,B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1 100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A,B两种商品很快售完,威丽商场决定再一次购进A,B两种商品共34件.如果将这34件商品全部售完后所得利润不低于4 000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
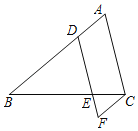
查看答案和解析>>【题目】如图,D,E分别是三角形ABC的边AB,BC上的点,DE∥AC,点F在DE的延长线上,且∠DFC=∠A.
(1)求证:AB∥CF;
(2)若∠ACF比∠BDE大40°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
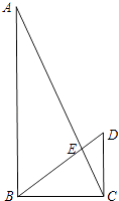
(1)求BE的长度;
(2)求△ABE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一商店在某一时间以每件a元(a>0)的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%.
(1)当a=60时,分析卖出这两件衣服总的是盈利还是亏损,或是不盈不亏?
(2)小安发现:不论a为何值,这样卖两件衣服总的都是亏损.请判断“小安发现”是否正确?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,射线OC在∠A0B的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“定分线”
(1)一个角的平分线______这个角的“定分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=
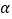 ,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)(3)如图2,若∠MPN=45°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成90°时停止旋转,旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.当PQ是∠MPN的“定分线”时,求t的值。

相关试题

