【题目】如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,BE=3cm,AD=9cm.
求:(1)DE的长;
(2)若CE在△ABC的外部(如图),其它条件不变,DE的长是多少?

参考答案:
【答案】(1)DE= 6cm;(2)DE= 12cm.
【解析】试题分析:(1)由余角的性质,推出∠CBE=∠ECA,再依据全等三角形的判定定理“AAS”,推出△BEC和△CDA全等,然后即得BE=CD,CE=AD,再由BE=3cm,AD=9cm,结合图形即可推出DE=6cm,(2)根据余角的性质推出∠CBE=∠ACD,再依据全等三角形的判定定理“AAS”,推出△BEC和△CDA全等,然后即得BE=CD,CE=AD,再由BE=3cm,AD=9cm,结合图形即可推出DE=12cm.
试题解析:解:(1)∵∠ACB=90°,BE⊥CE,∴∠BCE+∠CBE=90°,∠BCE+∠ECA=90°,∴∠CBE=∠ECA,∠BEC=∠CDA.在△BEC和△CDA中,∵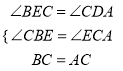 ,∴△BEC≌△CDA(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴CD=3cm,CE=9cm,∴DE=CE﹣CD=6cm.
,∴△BEC≌△CDA(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴CD=3cm,CE=9cm,∴DE=CE﹣CD=6cm.
(2)∵∠ACB=90°,BE⊥CE于E,AD⊥CE于D,∴∠BCE+∠CBE=90°,∠BCE+∠DCA=90°,∠BEC=∠CDA=90°,∴∠CBE=∠ACD.在△CBE和△ACD中,∵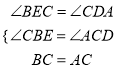 ,∴△CBE≌△ACD(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴DE=CD+CE=BE+AD=12cm.
,∴△CBE≌△ACD(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴DE=CD+CE=BE+AD=12cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.

(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥ED于点E,求∠AOD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.小张用骑公共自行车方式上班平均每小时行驶多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读思考
我们知道,在数轴上|a|表示数a所对应的点到原点的距离,这是绝对值的几何意义,由此我们可进一步地来研究数轴上任意两个点之间的距离,一般地,如果数轴上两点A、B 对立的数用a,b表示,那么这两个点之间的距离AB=|a﹣b|.也可以用两点中右边的点所表示数的减去左边的点所表示的数来计算,例如:数轴上P,Q两点表示的数分别是﹣1和2,那么P,Q两点之间的距离就是 PQ=2﹣(﹣1)=3.
启发应用
如图,点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0
(1)求线段AB的长;
(2)如图,点C在数轴上对应的数为x,且x是方程2x+1=
 x﹣8的解,
x﹣8的解,①求线段BC的长;
②在数轴上是否存在点P使PA+PB=BC?若存在,直接写出点P对应的数:若不存在,说明理由.
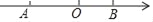
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.

(1)已知旗杆高为12米,若在点B处测得旗杆顶点E的仰角为30°,A处测得点E的仰角为45°,试求AB的长(结果保留根号);
(2)在(1)的条件下,若∠BCA=45°,绳子在空中视为一条线段,试求绳子AC的长(结果保留根号)? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB//DE,AC//DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )

A. AB=DE B. EF=BC C. ∠B=∠E D. EF∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线y=2x﹣2与曲线y=
 (x>0)相交于点A(2,n),与x轴、y轴分别交于点B,C.
(x>0)相交于点A(2,n),与x轴、y轴分别交于点B,C.
(1)求曲线的解析式;
(2)试求ABAC的值?
(3)如图2,点E是y轴正半轴上一动点,过点E作直线AC的平行线,分别交x轴于点F,交曲线于点D.是否存在一个常数k,始终满足:DEDF=k?如果存在,请求出这个常数k;如果不存在,请说明理由.
相关试题

