Question

【题目】（1）如图①，一个无盖的长方体盒子的棱长分别为，，，盒子的内部顶点处有一只昆虫甲，在盒子的内部顶点处有一只昆虫乙（盒壁的厚度忽略不计）假设昆虫甲在顶点处静止不动，请计算处的昆虫乙沿盒子内壁爬行到昆虫甲处的最短路程，并画出其最短路径，简要说明画法

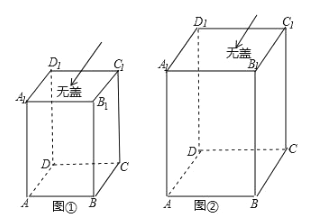
（2）如果（1）问中的长方体的棱长分别为，，如图②，假设昆虫甲从盒内顶点以1厘米/秒的速度在盒子的内部沿棱向下爬行，同时昆虫乙从盒内顶点以3厘米/秒的速度在盒壁的侧面上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？

Answer 1

【答案】（1）就是最短路径；（2）5秒

【解析】

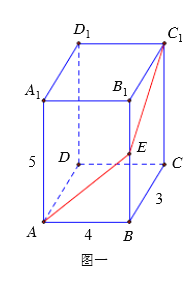
解：（1）如图二，将上表面展开，使上表面与前表面在同一平面内，即三点共线，，

根据勾股定理得

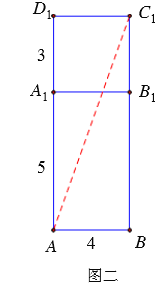
如图三，将右侧面展开，使右侧面与下面在同一平面内，即三点共线

，

根据勾股定理得

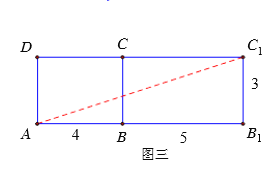
如图四，将右侧面展开，使右侧面与前表面在同一平面内，即三点共线.

，

根据勾股定理得

∵＜＜

∴最短路程是.

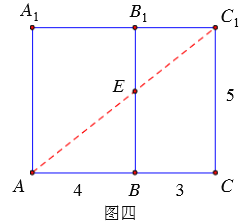
在图四中，∵

∴

∴，

如图一，在上取一点，使，连接，，就是最短路径

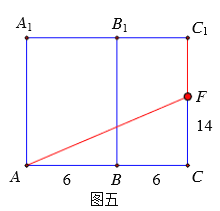
（2）如图五，设，则，

在中，根据勾股定理得

即：

解得：，

∵

∴

所以，昆虫至少需要5秒才能捉到昆虫甲.