【题目】如图，在△ABC中，AB=AC，AD是角平分线，BE平分∠ABC交AD于点E，点O在AB上，以OB为半径的⊙O经过点E，交AB于点F
（1）求证：AD是⊙O的切线；
（2）若AC=4，∠C=30°，求 的长．

参考答案：

【答案】
（1）证明：

如图，连接OE，

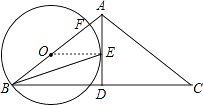
∵OB=OE，

∴∠OBE=∠OEB，

∵BE平分∠ABC，

∴∠OBE=∠EBD，

∴∠OEB=∠EBD，

∴OE∥BD，

∵AB=AC，AD平分∠BAC，

∴AD⊥BC，

∴∠OEA=∠BDA=90°，

∴AD是⊙O的切线


（2）解：∵AB=AC=4，∠C=∠B=30°，

∴BD=2 ，

设圆的半径为r，则BO=OE=r，AO=AC﹣OB=4﹣r，

∵OE∥BD，

∴ = ，即 = ，解得r=8 ﹣12，

∴ = =


【解析】（1）连接OE，利用角平分线的定义和圆的性质可得∠OBE=∠OEB=∠EBD，可证明OE∥BD，结合等腰三角形的性质可得AD⊥BD，可证得OE⊥AD，可证得AD为切线；（2）利用（1）的结论，结合条件可求得∠AOE=30°，由（1）可知OE∥BD，设半径为r，则OB=OE=r，AO=4﹣r，在Rt△ABD中，由勾股定理可求得BD，由平行线分线段成比例可得到关于r的方程，可求得圆的半径，利用弧长公式可求得 ．
【考点精析】认真审题，首先需要了解等腰三角形的性质(等腰三角形的两个底角相等（简称：等边对等角）)，还要掌握含30度角的直角三角形(在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半)的相关知识才是答题的关键．

关闭