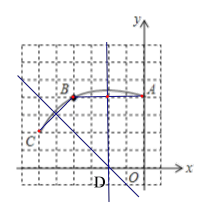
[题目]如图.在正方形网格图中建立平面直角坐标系.一条圆弧经过格点...若该圆弧所在圆的圆心为点.请你利用网格图回答下列问题:(1)圆心的坐标为 ,(2)若扇形是一个圆锥的侧面展开图.求该圆锥底面圆的半径长．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在正方形网格图中建立平面直角坐标系，一条圆弧经过格点、、，若该圆弧所在圆的圆心为点，请你利用网格图回答下列问题：

（1）圆心的坐标为_____；

（2）若扇形是一个圆锥的侧面展开图，求该圆锥底面圆的半径长（结果保留根号）．

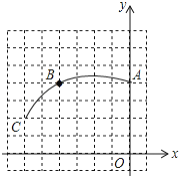
【答案】（1）；（2）该圆锥底面圆的半径长为．

【解析】

（1）连接、，分别作、的垂直平分线，两直线交于点，则点即为该圆弧所在圆的圆心，进而即可求解；

（2）根据网格结构，可得，，根据勾股定理的逆定理，可得，结合弧长公式与圆周长公式，即可求解．

（1）连接、，分别作、的垂直平分线，两直线交于点，则点即为该圆弧所在圆的圆心，可知点的坐标为．

故答案是：；

（2）∵圆的半径长．

∴，，

，

．

设圆锥的底面圆的半径长为，

∴，

解得：，

答：该圆锥底面圆的半径长为．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在某一路段，规定汽车限速行驶，交通警察在此限速路段的道路上设置了监测区，其中点C、D为监测点，已知点C、D、B在同一直线上，且AC⊥BC，CD＝400米，tan∠ADC＝2，∠ABC＝35°

（1）求道路AB段的长（结果精确到1米）

（2）如果道路AB的限速为60千米/时，一辆汽车通过AB段的时间为90秒，请你判断该车是否是超速，并说明理由；参考数据：sin35°≈0.5736，cos35°≈0.8192，tan35°≈0.7002

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】规定：sin（﹣x）=﹣sinx，cos（﹣x）=cosx，sin（x+y）=sinxcosy+cosxsiny．

据此判断下列等式成立的是（写出所有正确的序号）

①cos（﹣60°）=﹣；

②sin75°=；

③sin2x=2sinxcosx；

④sin（x﹣y）=sinxcosy﹣cosxsiny．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知在平面直角坐标系中，点A（0，3），点B为x轴上一动点，连接AB，线段AB绕着点B按顺时针方向旋转90°至线段CB，过点C作直线l∥y轴，在直线l上有一点D位于点C下方，满足CD＝BO，则当点B从（﹣3，0）平移到（3，0）的过程中，点D的运动路径长为_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】将一副三角尺按如图①方式拼接：含30°角的三角尺的长直角边与含45°角的三角尺的斜边恰好重合（在Rt△ABC中，∠ACB＝90°，∠BAC＝30°；在Rt△ACD中，∠ADC＝90°∠DAC＝45°）已知AB＝2，P是AC上的一个动点．

（1）当PD＝BC时，求∠PDA的度数；

（2）如图②，若E是CD的中点，求△DEP周长的最小值；

（3）如图③，当DP平分∠ADC时，在△ABC内存在一点Q，使得∠DQC＝∠DPC，且CQ＝，求PQ的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，按以下步骤作图：①分别以点A和点C为圆心，以大于AC的长为半径作弧，两弧相交于M、N两点；②作直线MN交BC于点D，连接AD．若AB＝BD，AB＝4，∠C＝30°，则△ACD的面积为（）

A.B.C.D.13

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某单位有职工200人，其中青年职工（20﹣35岁），中年职工（35﹣50岁），老年职工（50岁及以上）所占比例如扇形统计图所示．

为了解该单位职工的健康情况，小张、小王和小李各自对单位职工进行了抽样调查，将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3．

表1：小张抽样调查单位3名职工的健康指数

年龄	26	42	57
健康指数	97	79	72

表2：小王抽样调查单位10名职工的健康指数

年龄	23	25	26	32	33	37	39	42	48	52
健康指数	93	89	90	83	79	75	80	69	68	60

表3：小李抽样调查单位10名职工的健康指数

年龄	22	29	31	36	39	40	43	46	51	55
健康指数	94	90	88	85	82	78	72	76	62	60

根据上述材料回答问题：

（1）小张、小王和小李三人中，谁的抽样调查的数据能够较好地反映出该单位职工健康情况，并简要说明其他两位同学抽样调查的不足之处．

（2）根据能够较好地反映出该单位职工健康情况表，绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为出行方便，近日来越来越多的重庆市民使用起了共享单车，图1为单车实物图，图2为单车示意图，AB与地面平行，点A、B、D共线，点D、F、G共线，坐垫C可沿射线BE方向调节．已知∠ABE=70°，∠EAB=45°，车轮半径为30cm，BE=40cm．小明体验后觉得当坐垫C离地面高度为0.9m时，骑着比较舒适，此时CE的长约为（）（结果精确到1cm，参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75，≈1.41）