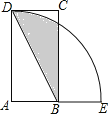
【题目】如图，四边形ABCD为矩形，以A为圆心，AD为半径的弧交AB的延长线于点E，连接BD，若AD=2AB=4，则图中阴影部分的面积为______．

【答案】π+2-4

【解析】

BC交弧DE于F，连接AF，如图，先利用三角函数得到∠AFB=30°，则∠BAF=60°，∠DAF=30°，BF=AB=2，然后根据三角形面积公式和扇形的面积公式，利用图中阴影部分的面积=S扇形ADF+S△ABF-S△ABD进行计算即可．

解：BC交弧DE于F，连接AF，如图，

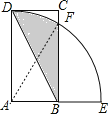
AF=AD=4，

∵AD=2AB=4

∴AB=2，

在Rt△ABF中，∵sin∠AFB==，

∴∠AFB=30°，

∴∠BAF=60°，∠DAF=30°，BF=AB=2，

∴图中阴影部分的面积=S扇形ADF+S△ABF-S△ABD

=+×2×2-×2×4

=π+2-4．

关闭