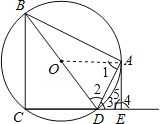
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.

(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
参考答案:
【答案】(1)证明见解析(2)![]() .
.
【解析】
试题分析:(1)连接OA,利用已知首先得出OA∥DE,进而证明OA⊥AE就能得到AE是⊙O的切线;
(2)通过证明△BAD∽△AED,再利用对应边成比例关系从而求出⊙O半径的长.
(1)证明:连接OA,
∵OA=OD,
∴∠1=∠2.
∵DA平分∠BDE,
∴∠2=∠3.
∴∠1=∠3.∴OA∥DE.
∴∠OAE=∠4,
∵AE⊥CD,∴∠4=90°.
∴∠OAE=90°,即OA⊥AE.
又∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:∵BD是⊙O的直径,
∴∠BAD=90°.
∵∠5=90°,∴∠BAD=∠5.
又∵∠2=∠3,∴△BAD∽△AED.
∴![]() ,
,
∵BA=4,AE=2,∴BD=2AD.
在Rt△BAD中,根据勾股定理,
得BD=![]() .
.
∴⊙O半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:9x2﹣6x+1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三个顶点距离相等的点是( )
A. 三条边的中线的交点 B. 三条高线的交点
C. 三条边的垂直平分线的交点 D. 三条角平分线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A.有两条边相等的两个等腰三角形全等
B.两腰对应相等的两个等腰三角形全等
C.两角对应相等的两个等腰三角形全等
D.一边对应相等的两个等边三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O为Rt△ABC的内切圆,⊙O的半径r=1,∠B=30°,
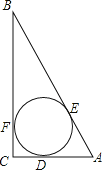
(1)劣弧DE的长.
(2)证明:AD=AE.
(3)求:劣弧DE、切线AD、AE所围成的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
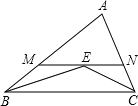
A.6 B.7 C.8 D.9
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组):
(1)10(x﹣3)﹣4≤2(x﹣1)
(2)x﹣
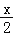 ﹣
﹣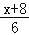 <1﹣
<1﹣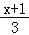
(3)
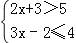
(4)
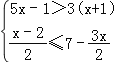 (在数轴上表示解集)
(在数轴上表示解集)
相关试题

