Question

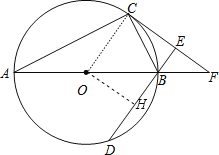
【题目】如图，AB为⊙O直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC．过点C作CE⊥DB，垂足为E，直线AB与CE相交于F点．

（1）求证：CF为⊙O的切线；

（2）若⊙O的半径为cm，弦BD的长为3cm，求CF的长．

考点：切线的判定．

Answer 1

【答案】

【解析】

试题分析:（1）连结OC，如图，由于∠A=∠OCA，则根据三角形外角性质得∠BOC=2∠A，而∠ABD=2∠BAC，所以∠ABD=∠BOC，根据平行线的判定得到OC∥BD，再CE⊥BD得到OC⊥CE，然后根据切线的判定定理得CF为⊙O的切线；

（2）解：作OH⊥BD于H，如图，根据垂径定理得到BH=DH=BD=，在Rt△OBH中可利用勾股定理计算出OH=2，易得四边形OHEC为矩形，则CE=OH=2，HE=OC=，BE=1，然后证明△FBE∽△FOC，利用相似比可计算出CF．

（1）证明：连结OC，如图，

∵OA=OC，

∴∠A=∠OCA，

∴∠BOC=∠A+∠OCA=2∠A，

∵∠ABD=2∠BAC，

∴∠ABD=∠BOC，

∴OC∥BD，

∵CE⊥BD，

∴OC⊥CE，

∴CF为⊙O的切线；

（2）解：作OH⊥BD于H，如图，

则BH=DH=BD=，

在Rt△OBH中，∵OB=，BH=，

∴OH==2，

易得四边形OHEC为矩形，

∴CE=OH=2，HE=OC=，

∴BE=NE﹣BH=1，

∵BE∥OC，

∴△FBE∽△FOC，

∴=，即=，

∴CF=．