【题目】某水果店经销A、B两种水果，A种水果进货单价比B种水果进货单价多2元，花50元购进A种水果的数量与花40元购进B种水果的数量相同．在销售过程中发现，A种水果每天销售量是
与销售价x（元）满足关系式
，B种水果，每天销售量
与销售价x（元）满足= -x+14
（1）求A、B两种水果的单价．
（2）已知A种水果比B种水果的销售价高2元/千克，且每天A、B水果均有a千克坏掉．设B水果售价为t元/千克，每天两种水果的总利润为W元，求W与t的函数解析式，并求出当a的取值在什么范围内，水果店有可能不赔钱？
【答案】（1）A种水果10元/千克，B种水果8元/千克；（2）a不超过
时，水果可能不赔钱
【解析】
（1）设水果B的进货单价为
元/千克，则水果A的进货单价为(
)元/千克，根据“花50元购进A种水果的数量与花40元购进B种水果的数量相同”列方程解答即可；
（2）根据总利润
A，B两种水果的利润和减去损耗，列出函数表达式，配方成顶点式，由二次函数性质即可得出答案．
答案：（1）设水果B的进货单价为元/千克，则水果A的进货单价为()元/千克，
依题意得：
，
解得：
，
检验：经检验
是原方程的解．
∴，
∴
，
答：A种水果10元/千克，B种水果8元/千克；
（2）设B水果售价为
元/千克，则A水果售价为(
)元/千克，
，
∵ -2＜0
∴
时，W（最大）
，
当
时，
．
答：
不超过时，水果可能不赔钱．
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案科目：初中数学 来源： 题型：
【题目】如图1，抛物线
与两条坐标轴分别交于
，
，
三点．其中
，且
．
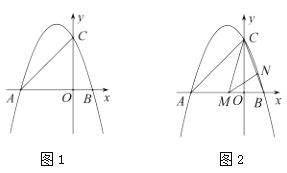
（1）求该抛物线的解析式；
（2）点
是
轴上一点，抛物线上是否存在点
，使得以点，，，为顶点，以
为边的四边形是平行四边形？若存在，求出点的坐标；若不存在，请说明理由；
（3）如图2，点
，
分别是线段
，
上的动点，连接
，
，当
时，求点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
是
的外接圆，AD为的直径，
，垂足为E，连接BO，延长BO交AC于点F．
（1）如图1，求证：
；
（2）如图2，过点D作
，交于点G，点H为GD的中点，连接OH，求证：
；
（3）如图3，在（2）的条件下，连接CG，若
的面积为
，求线段CG的长．
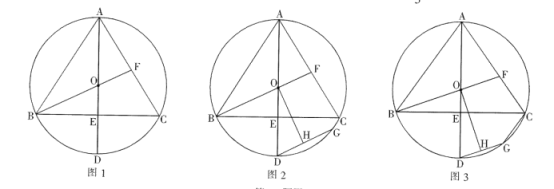
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，函数y=
（x＞0）的图象与直线y=mx交于点A（2，2）．
（1）求k，m的值；
（2）点P的横坐标为n（n＞0），且在直线y=mx上，过点P作平行于x轴的直线，交y轴于点M，交函数y=（x＞0）的图象于点N．
①n=1时，用等式表示线段PM与PN的数量关系，并说明理由；
②若PN≥3PM，结合函数的图象，直接写出n的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下图为我市某校2015年参加各类比赛（包括围棋、书法、绘画、钢琴四个类别）的参赛人数统计图：
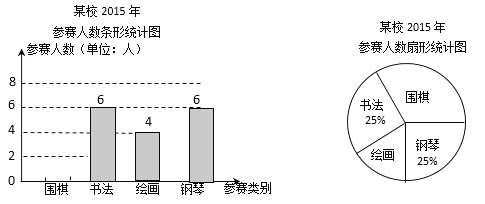
（1）该校参加比赛的总人数是 人，并把条形统计图补充完整；
（2）在扇形统计图中，该校参加围棋所对应的圆心角的度数是 ；
（3）从全市中小学参加比赛选手中随机抽取60人，其中有20人获奖．今年我市中小学参加比赛人数共有2400人，请你估算今年参加绘画比赛的人数以及参加比赛获奖的总人数约是多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2020年是脱贫攻坚年，为实现全员脱贫目标，某村贫困户在当地政府支持帮助下，办起了养鸡场，经过一段时间精心饲养，总量为3000只的一批鸡可以出售．现从中随机抽取50只，得到它们质量的统计数据如下：
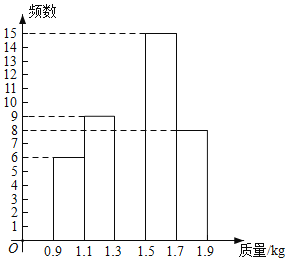
质量 | 组中值 | 数量（只） |
| 1.0 | 6 |
| 1.2 | 9 |
| 1.4 | a |
| 1.6 | 15 |
| 1.8 | 8 |
根据以上信息，解答下列问题：
（1）表中
______，补全频数分布直方图；
（2）这批鸡中质量不小于
的大约有多少只？
（3）这些贫因户的总收入达到54000元，就能实现全员脱贫目标．按15元
的价格售出这批鸡后，该村贫困户能否脱贫？
查看答案和解析>>
科目：初中数学 来源： 题型：
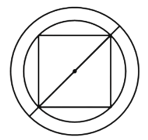
【题目】据《汉书律历志》记载：“量者，龠（yuè）、合、升、斗、斛（hú）也”斛是中国古代的一种量器，“斛底，方而圜（huán）其外，旁有庣（tiāo）焉”．意思是说：“斛的底面为：正方形的外接一个圆，此圆外是一个同心圆”，如图所示．
问题：现有一斛，其底面的外圆直径为两尺五寸（即2.5尺），“庣旁”为两寸五分（即两同心圆的外圆与内圆的半径之差为0.25尺），则此斛底面的正方形的周长为________尺．（结果用最简根式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
●操作发现：
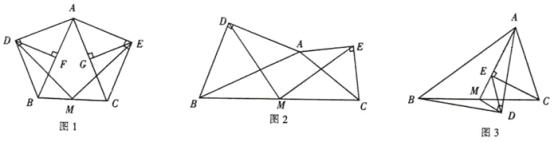
在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是 （填序号即可）
①AF=AG=
AB；②MD=ME；③整个图形是轴对称图形；④∠DAB=∠DMB．
●数学思考：
在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量和位置关系？请给出证明过程；
●类比探索：
在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．
答： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
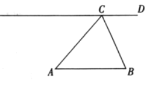
【题目】已知：如图，
ABC为锐角三角形，AB=BC，CD∥AB．
求作：线段BP，使得点P在直线CD上，且∠ABP=
．
作法：①以点A为圆心，AC长为半径画圆，交直线CD于C，P两点；②连接BP．线段BP就是所求作线段．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）
（2）完成下面的证明．
证明：∵CD∥AB，
∴∠ABP= ．
∵AB=AC，
∴点B在⊙A上．
又∵∠BPC=
∠BAC（ ）（填推理依据）
∴∠ABP=∠BAC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
