【题目】如图,一次函数y=﹣![]() x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
(1)求m的值及点E、F的坐标;
(2)求△APE的面积;
(3)若B点是x轴上的动点,问在直线EF上,是否存在点Q(Q与A不重合),使△BEQ与△APE全等?若存在,请求出点Q的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)m=![]() ,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(
,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,﹣
,﹣![]() ),Q3(
),Q3(![]() ,﹣2).
,﹣2).
【解析】
(1)根据函数值,可得相应自变量的值,根据自变量的值,可得相应的函数值;
(2)根据待定系数法,可得AP的解析式,根据函数值为零,可得P点坐标,根据三角形的面积公式,可得答案;
(3)分类讨论:①当点A与点B为对应顶点时,根据全等三角形的面积相等,可得Q点的纵坐标,根据函数值,可得相应自变量的值;②当点A与点Q为对应顶点时,可得Q点的纵坐标,根据函数值,可得相应自变量的值.
解:(1)一次函数y=﹣![]() x+4的图象经过点A(m,2),
x+4的图象经过点A(m,2),
得﹣![]() m+4=2,
m+4=2,
解得m=![]() ,
,
∵一次函数y=﹣![]() x+4的图象分别与x轴、y轴的正半轴交于点E,F.
x+4的图象分别与x轴、y轴的正半轴交于点E,F.
∴当y=0时,﹣![]() x+4=0,解得x=3即E(3,0);
x+4=0,解得x=3即E(3,0);
当x=0时,y=4,即F(0,4);
(2)把点A(![]() ,2)一次函数y=kx﹣4,得2=
,2)一次函数y=kx﹣4,得2=![]() k﹣4,解得k=4,
k﹣4,解得k=4,
y=4x﹣4,当y=0时,x=1,即P(1,0).
PE=3﹣1=2,
S△APE=![]() ×2×2=2;
×2×2=2;
(3)存在Q点,B点是x轴上的动点,点Q是直线y=﹣![]() x+4上的点,设Q(m,n).
x+4上的点,设Q(m,n).
由两点间的距离,得AE=![]() =
=![]() ,AP=
,AP=![]() =
=![]() ,PE=2.
,PE=2.
①当点A与点B为对应顶点时,
∵△APE≌△BQE,
∴S△BQE=S△APE=2,
∴![]() BE×|n|=2.
BE×|n|=2.
∵BE=AE=![]() ,
,
∴|n|=![]() ,n=±
,n=±![]() .
.
当n=![]() 时,﹣
时,﹣![]() x+4=
x+4=![]() ,解得m=
,解得m=![]() ,即Q1(
,即Q1(![]() ,
,![]() );
);
当n=﹣![]() 时,﹣
时,﹣![]() x+4=﹣
x+4=﹣![]() ,解得m=
,解得m=![]() ,即Q2(
,即Q2(![]() ,﹣
,﹣![]() );
);
②当点A与点Q为对应顶点时,∵△APE≌△QBE,
则n=﹣2,把n=﹣2代入y=﹣![]() x+4得m=
x+4得m=![]() ,
,
∴Q3(![]() ,﹣2),
,﹣2),
综上所述:Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,﹣
,﹣![]() ),Q3(
),Q3(![]() ,﹣2).
,﹣2).

故答案为:(1)m=![]() ,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(
,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,﹣
,﹣![]() ),Q3(
),Q3(![]() ,﹣2).
,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

-
科目: 来源: 题型:
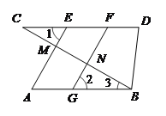
查看答案和解析>>【题目】已知:如图,AE⊥BC于M,FG⊥BC于N,∠1=∠2
(1)求证:AB∥CD;(2)若∠D=∠3+50°,∠CBD=70°,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级
中位数(分)
众数(分)
平均数(分)
爱国班
85
求知班
100
85
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?

-
科目: 来源: 题型:
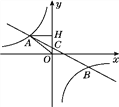
查看答案和解析>>【题目】【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
-
科目: 来源: 题型:
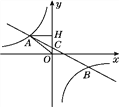
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
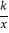 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
【答案】(1)△AHO的周长为12;(2) 反比例函数的解析式为y=
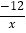 ,一次函数的解析式为y=-
,一次函数的解析式为y=- x+1.
x+1.【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=
 ,得
,得AH=4.即A(-4,3).
由勾股定理,得
AO=
 =5,
=5,△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=
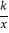 (k≠0),得
(k≠0),得k=-4×3=-12,
反比例函数的解析式为y=
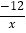 ;
;当y=-2时,-2=
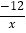 ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).将A、B点坐标代入y=ax+b,得
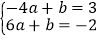 ,
,解得
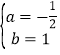 ,
,一次函数的解析式为y=-
 x+1.
x+1.考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
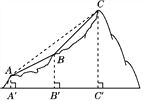
23【题目】如图,点A,B,C表示某旅游景区三个缆车站的位置,线段AB,BC表示连接缆车站的钢缆,已知A,B,C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米,310米,710米,钢缆AB的坡度i1=1∶2,钢缆BC的坡度i2=1∶1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B.
 C.
C.  D. 2
D. 2
相关试题

