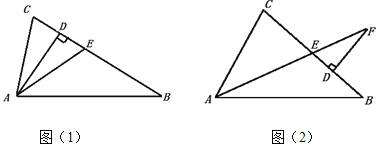
【题目】(1)如图(1),在△ABC中,AD、AE分别是△ABC的高和角平分线,已知:∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图(2),∠BAC的角平分线AF交BC于点E,过点F作FD⊥BC于点D,若∠B = x°,∠C =(x+30)° .
①∠CAE = (含x的代数式表示)②求∠F的度数.
参考答案:
【答案】(1)∠DAE = 10° ;(2) ①∠CAE = (75-x) °,② ∠F =15°
【解析】试题分析:(1)先根据三角形内角和得到∠CAB=180°-∠B-∠C=100°,再根据角平分线与高线的定义得到∠CAE=![]() ∠CAB=50°,∠ADC=90°,则∠CAD=90°-∠C=40°,然后利用∠DAE=∠CAE-∠CAD计算即可;
∠CAB=50°,∠ADC=90°,则∠CAD=90°-∠C=40°,然后利用∠DAE=∠CAE-∠CAD计算即可;
(2)根据题意可知∠B=x°,∠C=(x+30)°,根据三角形的内角和定理可知∠ADC+∠DAC+∠C=180°,∠ADC=∠B+∠BAF,根据角平分线的性质,可知∠EAC=∠BAF,可得出∠ADC的度数,再根据FD⊥BC,可得出∠F的度数.
试题解析:(1)∵∠B=30°,∠C=50°,
∴∠CAB=180°-∠B-∠C=100°,
∵AD是△ABC角平分线,
∴∠CAE=![]() ∠CAB=50°,
∠CAB=50°,
∵AE是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°-∠C=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°;
(2)①∵∠B=x°,∠C=(x+30)°,AF平分∠BAC,
∴∠EAC=∠BAF,
∴∠CAE=![]() ×[180°-x°-(x+30)°]=75°-x°,
×[180°-x°-(x+30)°]=75°-x°,
②∠AEC=∠BAE+∠B=75°,
∵FD⊥BC,
∴∠F=15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C; ②∠AEF=∠AFE; ③∠EBC=∠C;④AG⊥EF.正确结论有( )
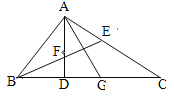
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. x4+x2=x6 B. x2x3=x6 C. (x2)3=x6 D. x2﹣y2=(x﹣y)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某风景区集体门票的收费标准是:20人以内(含20人)每人25元;超过20人的,超过的人数每人l0元.对有x人(x大于或等于20人)的旅行团,应收多少门票费?(用含x式子表示,并化简).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(列方程计算)某数的5倍减去4,比该数大4,求这个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】时光飞逝,小学、中学的学习时光已过去,九年的在校时间大约有16200小时,请将数16200用科学记数法表示为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个过点(0,-2),且函数值y随自变量x的增大而减小的一次函数关系式:_______________.(填上一个答案即可)
相关试题

