搜索
【题目】仔细观察图形，认真分析下列各式，然后解答问题.
OA
＝(
)2＋1＝2，S1＝
；
OA
＝(
)2＋1＝3，S2＝
；
OA
＝(
)2＋1＝4，S3＝
；
…
求：(1)请用含有n(n是正整数)的等式表示上述变化规律；
(2)推算出OA10的长；
(3)求出S
＋S＋S＋…＋S
的值．
参考答案：
【答案】(1) 
,Sn＝
(n为正整数)；（2）
；（3）
.
【解析】
（1）根据题意可知当n为正整数时，OAn2=（
）2+1，Sn=
；
（2）把n=10，代入到（1）所推出的结论即可求出OA10的值；
（3）把n=1，2，3…10，分别代入到（1）所推出的结论Sn=，即可求出S12，S22，S32，…S102的值，即可推出结果．
解：(1)
＝()2＋1＝n，Sn＝(n为正整数)．
(2)∵
＝10，
∴OA10＝；
(3) S12＋S22＋S32＋…＋S102
＝(
)2＋(
)2＋(
)2＋…＋(
)2＋(
)2
＝
＋
＋
＋…＋
＋
＝
＝
＝.
-
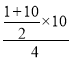
科目： 来源： 题型：
查看答案和解析>>【题目】威丽商场销售A、B两种商品，售出1件A种商品和4件B种商品所得利润为600元；售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元？
(2)由于需求量大，A、B两种商品很快售完，威丽商场决定再一次购进A、B两种商品共34件，如果将这34件商品全部售完后所得利润不低于4000元，那么威丽商场至少需购进多少件A种商品？
-
科目： 来源： 题型：
查看答案和解析>>【题目】用一条长为18cm的细绳围成一个等腰三角形.
（1）如果腰长是底边长的2倍，求三角形各边的长；
（2）能围成有一边的长是4cm的等腰三角形吗？若能，求出其他两边的长；若不能，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一艘船由A港沿北偏东60°方向航行10km至B港，然后再沿北偏西30°方向航行10km至C港．
（1）求A，C两港之间的距离（结果保留到0.1km，参考数据：
≈1.414，
≈1.732）；（2）确定C港在A港的什么方向．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE
（1）求证：CE=AD
（2）当点D在AB中点时，四边形BECD是什么特殊四边形？说明理由
（3）若D为AB的中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料；
课堂上，老师设计了一个活动：将一个4×4的正方形网格沿着网格线划分成两部分（分别用阴影和空白表示），使得这两部分图形是全等的，请同学们尝试给出划分的方法．约定：如果两位同学的划分结果经过旋转、翻折后能够重合，那么就认为他们的划分方法相同．
小方、小易和小红分别对网格进行了划分，结果如图①、图②、图③所示．
小方说：“我们三个人的划分方法都是正确的，但是将小红的整个图形（图③）逆时针旋转90
后得到的划分方法与我的划分方法（图①）是一样的，应该认为是同一种方法，而小易的划分方法与我的不同，”老师说：“小方说得对．”
完成下列问题：
(1)图④的划分方法是否正确？
(2)判断图⑤的划分方法与图②小易的划分方法是否相同，并说明你的理由．
(3)请你再想出一种与已有方法不同的划分方法，使之满足上述条件，并在图⑥中画出来．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，有一张矩形纸片ABCD，AB＝4，BC＝8，点M，N分别在矩形的边AD，BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P，点D落在G处，连接PC，交MN于点Q，连接CM．
（1）求证：四边形CMPN是菱形；
（2）当P，A重合时，如图2，求MN的长；
（3）设△PQM的面积为S，求S的取值范围．
相关试题
