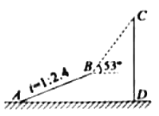
【题目】某兴趣小组为了测量大楼的高度，先沿着斜坡走了米到达坡顶点处，然后在点处测得大楼顶点的仰角为，已知斜坡的坡度为，点到大楼的距离为米，求大楼的高度．（参考数据：，，）

【答案】大楼的高度为52米

【解析】

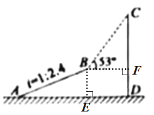
过点B作BE⊥AD于点E，作BF⊥CD于点F，在Rt△ABE中，根据坡度及勾股定理求出BE和AE的长，进而由三个角是直角的四边形是矩形判断四边形BEDF是矩形，得到BF和FD的长，再在Rt△BCF中，根据∠CBF的正切函数解直角三角形，得到CF的长，由CD=CF+FD得解．

解：如下图，过点B作BE⊥AD于点E，作BF⊥CD于点F，

在Rt△ABE中，AB=52，

∵

∴tan∠BAE==，

∴AE=2.4BE，

又∵BE2+AE2=AB2，

∴BE2+(2.4BE)2=522，

解得：BE=20，

∴AE=2.4BE=48；

∵∠BED=∠D=∠BFD=90°，

∴四边形BEDF是矩形，

∴FD=BE=20，BF=ED=AD-AE=72-48=24；

在Rt△BCF中，

tan∠CBF=，

即：tan53°==

∴CF=BF=32，

∴CD=CF+FD=32+20=52．

答：大楼的高度为52米．

关闭