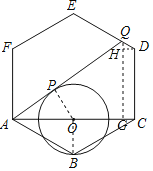
【题目】婷婷在发现一个门环的示意图如图所示．图中以正六边形ABCDEF的对角线AC的中点O为圆心，OB为半径作⊙O，AQ切⊙O于点P，并交DE于点Q，若AQ＝12cm，则该圆的半径为_____cm．

【答案】

【解析】

连接OB，OP，根据等腰三角形的性质得到OB⊥AC，根据切线的性质得到OP⊥AQ，设该圆的半径为r，得到OB＝OP＝r，根据等边三角形的性质得到AB＝BC＝CD＝2r，AO＝，求得AC＝，根据三角函数的定义得到sin∠PAO＝，过Q作QG⊥AC于G，过D作DH⊥QG于H，根据矩形的性质得到HG＝CD，DH＝CG，∠HDC＝90°，根据勾股定理得到AG＝，根据三角函数的定义即可得到结论．

解：连接OB，OP，

∵AB＝BC，O为AC的中点，

∴OB⊥AC，

∵AQ是⊙O的切线，

∴OP⊥AQ，

设该圆的半径为r，

∴OB＝OP＝r，

∵∠ABC＝120°，

∴∠BAO＝30°，

∴AB＝BC＝CD＝2r，AO＝，

∴AC＝，

∴sin∠PAO＝，

过Q作QG⊥AC于G，过D作DH⊥QG于H，

则四边形DHGC是矩形，

∴HG＝CD，DH＝CG，∠HDC＝90°，

∴sin∠PAO＝，∠QDH＝120°﹣90°＝30°，

∴QG＝12，

∴AG＝，

∴QH＝12﹣2r，DH＝，

∴tan∠QDH＝tan30°＝，

解得r＝，

∴该圆的半径为cm，

故答案为：．

关闭