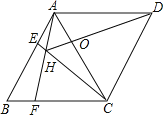
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
A.①② B.①③ C.②③ D.①②③
参考答案:
【答案】D
【解析】
试题分析:由菱形ABCD中,AB=AC,易证得△ABC是等边三角形,则可得∠B=∠EAC=60°,由SAS即可证得△ABF≌△CAE;则可得∠BAF=∠ACE,利用三角形外角的性质,即可求得∠AHC=120°;在HD上截取HK=AH,连接AK,易得点A,H,C,D四点共圆,则可证得△AHK是等边三角形,然后由AAS即可证得△AKD≌△AHC,则可证得AH+CH=DH.
解:∵四边形ABCD是菱形,
∴AB=BC,
∵AB=AC,
∴AB=BC=AC,
即△ABC是等边三角形,
同理:△ADC是等边三角形
∴∠B=∠EAC=60°,
在△ABF和△CAE中,
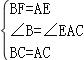 ,
,
∴△ABF≌△CAE(SAS);
故①正确;
∴∠BAF=∠ACE,
∵∠AEH=∠B+∠BCE,
∴∠AHC=∠BAF+∠AEH=∠BAF+∠B+∠BCE=∠B+∠ACE+∠BCE=∠B+∠ACB=60°+60°=120°;
故②正确;
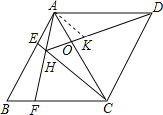
在HD上截取HK=AH,连接AK,
∵∠AHC+∠ADC=120°+60°=180°,
∴点A,H,C,D四点共圆,
∴∠AHD=∠ACD=60°,∠ACH=∠ADH,
∴△AHK是等边三角形,
∴AK=AH,∠AKH=60°,
∴∠AKD=∠AHC=120°,
在△AKD和△AHC中,
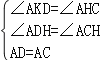 ,
,
∴△AKD≌△AHC(AAS),
∴CH=DK,
∴DH=HK+DK=AH+CH;
故③正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A.200(1+a%)2=148
B.200(1-a%)2=148
C.200(1-2a%)=148
D.200(1-a2%)=148 -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A. 1:2:3:4 B. 1:2:1:2 C. 1:1:2:2 D. 1:2:2:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:

(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P.若点P向右平移x(x取整数)个单位长度后落在△A2B2C2的内部,请直接写出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
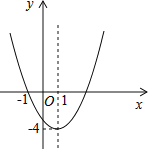
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D.当x<1时,y随x的增大而增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,全球每分钟约有8500000吨污水排入江河湖海,则每分钟的排污量用科学记数法表示应是___________吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平方根等于它本身的数是_____.
相关试题

