【题目】已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AB的中点,N是BC的中点,则线段MN的长度是.
参考答案:
【答案】3cm或7cm
【解析】∵M是AB的中点,N是BC的中点,
∴BM= ![]() AB=
AB= ![]() ×10=5cm,
×10=5cm,
BN= ![]() BC=
BC= ![]() ×4=2cm,
×4=2cm,
如图1,线段BC不在线段AB上时,MN=BM+BN=5+2=7cm,![]()
如图2,线段BC在线段AB上时,MN=BM-BN=5-2=3cm,![]()
综上所述,线段MN的长度是7cm或3cm.
【考点精析】认真审题,首先需要了解线段的中点(线段的中点到两端点的距离相等),还要掌握线段长短的计量(度量法:即用一把刻度量出两条线段的长度再比较;叠合法:从“形”的角度比较,观察点的位置)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM,ON分别是∠AOC,∠BOD的平分线,∠MON等于度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( )
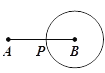
A.
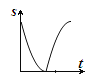 B.
B. 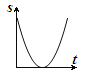 C.
C. 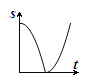 D.
D. 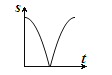
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣x2﹣2x+3的最大值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).

(1)用的代数式表示PC的长度;
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5a2b÷(﹣ ab)(2ab2)2
ab)(2ab2)2
(2)已知x2﹣5x﹣14=0,求(x﹣1)(2x﹣1)﹣(x+1)2+1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+y=6,xy=4,则x2y+xy2的值为_______.
相关试题

