【题目】如图,某地在山区修建高速公路时需挖通一条隧道,为估计这条隧道的长度需测出这座山A、B间的距离,结合所学知识或方法,设计测量方案你能给出什么好的方法吗?

参考答案:
【答案】见解析
【解析】
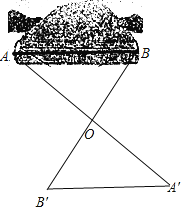
选择一合适的地点O,连接AO、BO,测出AO和BO的长度,延长AO、BO至A′、B′,使OA′=OA,OB′=OB,连接A′B′,则A′B′的长即是这座山A、B间的距离;可通过证△AOB≌△A′OB′来验证方案的合理性.
解:选择一合适的地点O,连接AO、BO,测出AO和BO的长度,延长AO、BO至A′、B′,使OA′=OA,OB′=OB,连接A′B′,这样就构成两个三角形,
在△AOB和△A′OB′中,
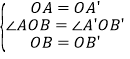 ,
,
∴△AOB≌△A′OB′(SAS),
∴AB=A′B′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚同学动手剪了如图①所示的正方形与长方形纸片若干张.

(1)他用1张1号、1张2号和2张3号卡片拼出一个新的图形(如图②).根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是 ;
(2)如果要拼成一个长为(a+2b),宽为(a+b)的大长方形,则需要2号卡片 张,3号卡片 张;
(3)当他拼成如图③所示的长方形,根据6张小纸片的面积和等于打纸片(长方形)的面积可以把多项式a2+3ab+2b2分解因式,其结果是 ;
(4)动手操作,请你依照小刚的方法,利用拼图分解因式a2+5ab+6b2= 画出拼图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小红学习了用图形面积研究整式乘法的方法后,分别进行了如下数学探究:把一根铁丝截成两段,
探究1:小明截成了两根长度不同的铁丝,并用两根不同长度的铁丝分别围成两个正方形,已知两正方形的边长和为20cm,它们的面积的差为40cm2,则这两个正方形的边长差为 .
探究2:小红截成了两根长度相同的铁丝,并用两根同样长的铁丝分别围成一个长方形与一个正方形,若长方形的长为xm,宽为ym,
(1)用含x、y的代数式表示正方形的边长为 ;
(2)设长方形的长大于宽,比较正方形与长方形面积哪个大,并说明理由.
-
科目: 来源: 题型:
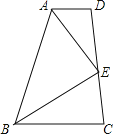
查看答案和解析>>【题目】已知四边形ABCD中,E是CD上的一点连接AE、BE,如图给出四个条件:①AE平分∠BAD,②BE平分∠ABC,③AE⊥EB,④AB=AD+BC,请你以其中三个作为命题的条件,写出一个能推出AD∥BC的正确命题,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x-1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.
分别计算下列各式的值:
(1)(x﹣1)(x+1)=x2﹣1;
(2)(x﹣1)(x2+x+1)=x3﹣1;
(3)(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= _________ ;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+297+…+2+1;
(2)(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1.
相关试题

