Question

【题目】如图，矩形ABCD的对角线AC与BD相交于点O，CE//BD，DE//AC.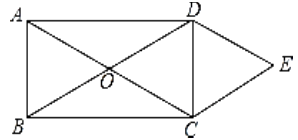

（1）求证：四边形OCED是菱形；
（2）当CD=6，DE=5，求AD的长.

Answer 1

【答案】
（1）

解：证明：∵CE//BD，DE//AC，

∴四边形OCED是平行四边形，

在矩形ABCD中，OD=OC，

∴四边形OCED是菱形.

（2）

解：在菱形OCED中，OC=DE=5，

又AC=2OC=10，

在Rt△ACD中，由勾股定理得AD= .

【解析】（1）先由CE//BD，DE//AC证得四边形OCED是平行四边形，再根据有一组邻边相等的平行四边形是菱形证得；（2）求出AC=2OC=2DE，由勾股定理即可求AD的长.
【考点精析】利用矩形的性质对题目进行判断即可得到答案，需要熟知矩形的四个角都是直角，矩形的对角线相等．