【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(﹣1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为 . 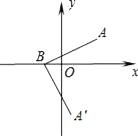
参考答案:
【答案】(1,﹣4)
【解析】解:作AC⊥x轴于C,
∵点A、B的坐标分别为(3,2)、(﹣1,0),
∴AC=2,BC=3+1=4,
把Rt△BAC绕点B顺时针旋转90°得到△BA′C′,如图,
∴BC′=BC=4,A′C′=AC=2,
∴点A′的坐标为(1,﹣4).
所以答案是(1,﹣4).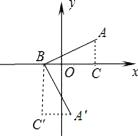
【考点精析】认真审题,首先需要了解图形的旋转(每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(﹣1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=x2向左平移2个单位得到的抛物线是( )
A.y=(x+2)2B.y=(x﹣2)2C.y=x2+2D.y=x2﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知∠A=∠F,∠C=∠D,按图填空,并在括号内注明理由.
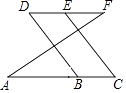
∵∠A=∠F()
∴∥()
∴∠D=∠ABD()
又∵∠D=∠C()
∴∠C=∠ABD()
∴∥() -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 两条对角线相等的四边形是平行四边形
B. 两条对角线相等且互相垂直的四边形是矩形
C. 两条对角线互相垂直平分的四边形是菱形
D. 两条对角线互相垂直平分且相等的四边形是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中正确的是( )
A. a3·a4=a12 B. (-a2)3=-a6 C. (ab)2=ab2 D. a8÷a4=a2
相关试题

