【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(-4,0),B(0,3),动点P从点O出发,沿x轴负方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造平行四边形PQCD,设点P运动的时间为t秒.
(1)当点Q在线段OB上时,用含t的代数式表示PC,AC的长;
(2)在运动过程中.
①当点D落在x轴上时,求出满足条件的t的值;
②若点D落在△ABO内部(不包括边界)时,直接写出t的取值范围;
(3)作点Q关于x轴的对称点Q′,连接CQ′,在运动过程中,是否存在某时刻使过A,P,C三点的圆与△CQQ′三边中的一条边相切?若存在,请求出t的值;若不存在,请说明理由.



参考答案:
【答案】(1)PC=![]() (4-t),AC=
(4-t),AC=![]() (4-t);(2)①
(4-t);(2)①![]() ,②
,②![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】试题分析:(1)首先求出AB,在Rt△ACP中,PA=4-t,根据sin∠OAB=![]() ,求出PC,根据cos∠OAB=
,求出PC,根据cos∠OAB=![]() ,求出AC.
,求出AC.
(2))①当D在x轴上时,由QC∥OA,得![]() ,由此即可解决问题.
,由此即可解决问题.
②当点D在AB上时,由PQ∥AB,得![]() ,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.
,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.
(3)当QC与⊙M相切时,则QC⊥CM,首先证明QB=QC,作QN⊥BC于N,根据cos∠ABO=![]() ,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似.
,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似.
试题解析:(1)如图1中,

∵OA=8,OB=6,∴AB=![]() =5.
=5.
在Rt△ACP中,PA=4-t,

∵sin∠OAB=![]() ,∴PC=
,∴PC=![]() (4-t),
(4-t),
∵cos∠OAB=![]() ,∴AC=
,∴AC=![]() (4-t).
(4-t).
(2)①当D在x轴上时,如图2中,
∵QC∥OA,∴![]() ∴
∴![]() ,
,
解得![]() .
.
∴![]() 时,点D在x轴上.
时,点D在x轴上.
②![]() .
.
(3)如图3中,

∵Q(0,3-2t),Q′(0,2t-3),
当QC与⊙M相切时,则QC⊥CM,
∴∠QCM=90°,∴∠QCP+∠PCM=90°,∵∠QCP+∠QCB=90°,
∴∠BCQ=∠PCM=∠CPM,
∵∠CPM+∠PAC=90°,∠OBA+∠OAB=90°,
∴∠APC=∠OBA,∴∠QBC=∠QCB,
∴BQ=CQ,作QN⊥BC于N,
∵cos∠ABO=![]() ,∴
,∴![]() ,
,
解得![]() ,
,
当CQ′是⊙M切线时,同理可得![]() ,解得
,解得![]() .
.
∴![]() 或
或![]() 时,过A,P,C三点的圆与△CQQ′三边中的一条边相切.
时,过A,P,C三点的圆与△CQQ′三边中的一条边相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣2x+3中,y的值随x值增大而__.(填“增大”或“减小”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:若x=2,y=﹣1,求2(x2y﹣xy2﹣1)﹣(2x2y﹣3xy2﹣3)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是【 】
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )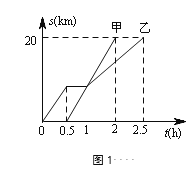
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学决定在八年级阳光体育“大课间”活动中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)将两个统计图补充完整;
(3)若调查到喜欢“立定跳远”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
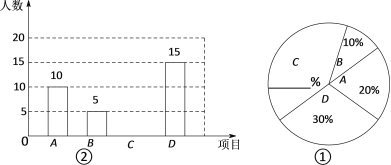
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列结论:(1)三点确定一个圆;(2)弧的度数指弧所对圆周角的度数;(3)三角形的内心是三边中垂线交点,它到三角形各边的距离相等;(4)同圆或等圆中,弦相等则弦所对的弧相等。其中正确的个数有( )
A. 0B. 1C. 3D. 2
相关试题

