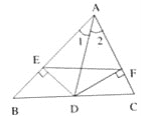
【题目】已知,如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高。求证:AD垂直平分EF。
参考答案:
【答案】见解析
【解析】
由DE⊥AB,DF⊥AC,得出∠AED=∠AFD;因为AD是△ABC的角平分线,可得∠1=∠2,DE=DF,推出△AED≌△AFD,即AE=AF,所以点A在EF的垂直平分线上,又DE=DF,推出点D在EF的垂直平分线上,即可证明AD垂直平分EF;
证明:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD,
又∵AD是△ABC的角平分线,
∴∠1=∠2,DE=DF,
∴△AED≌△AFD(AAS),
∴AE=AF,
∴点A在EF的垂直平分线上(到线段两端距离相等的点在线段的垂直平分线上),
∵DE=DF,
∴点D在EF的垂直平分线上,
∴AD垂直平分EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且EH=EB.下列四个结论:①∠ABC=45°;②AH=BC;③BE+CH=AE;④△AEC是等腰直角三角形.你认为正确的序号是( )

A. ①②③ B. ①③④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG=FC;③
 .
.其中正确的是

A. ①② B. ①③ C. ②③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是________.

-
科目: 来源: 题型:
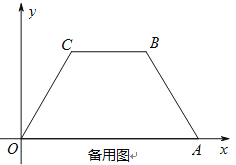
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC是等腰梯形,BC∥OA,OA=7,AB=4,∠ COA=60°,点P为x轴上的—个动点,点P不与点O、点A重合.连结CP,过点P作PD交AB于点D.
(1)求点B的坐标;
(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标;
(3)当点P运动什么位置时,使得∠CPD=∠OAB,且
 =
= ,求这时点P的坐标。
,求这时点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90o,AB=AD,AE=AC.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读题例,解答下题:
例解方程

解:
 当
当 ,即
,即 时
时
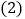 当
当 ,即
,即 时
时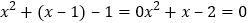
解得:
 不合题设,舍去
不合题设,舍去 ,
,
解得
 不合题设,舍去
不合题设,舍去
综上所述,原方程的解是
 或
或
依照上例解法,解方程
 .
.
相关试题

