【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作图:在△BED中作出BD边上的高EF;BE边上的高DG;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高EF为多少?若BE=6,求△BED中BE边上的高DG为多少?

参考答案:
【答案】(1)∠BED=55°;(2)画图见解析;(3)EF=4,DG=![]() .
.
【解析】试题分析:(1)根据三角形内角与外角的性质解答即可;
(2)过E作BC边的垂线,过D作BE边的垂线即可;
(3)根据三角形中线性质求出△BDE的面积,再由三角形的面积公式求出高即可.
试题解析:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)画图如下:

(3)∵AD为△ABC的中线,BE为△ABD的中线,
∴△ABD的面积=![]() △ABC的面积=20,△BDE的面积=
△ABC的面积=20,△BDE的面积=![]() △ABD的面积=10,
△ABD的面积=10,
∴![]() BD·EF=10,
BD·EF=10, ![]() ×5EF=10,
×5EF=10,
解得EF=4,
![]() BE·DG=10,
BE·DG=10, ![]() ×6 DG =10,
×6 DG =10,
EF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校就“遇见老人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查(每个被调查的学生必须选择而且只能在4种方式中选择一项),图1和图2是整理数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
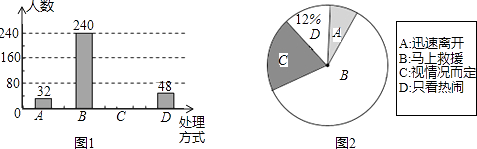
(1)该校随机抽查了名学生;
(2)将图1补充完整,在图2中,“视情况而定”部分所占的圆心角是度;
(3)估计该校2800名学生中采取“马上救助”的方式的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】|a|=(2017)0 , 则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b为有理数,且a>0,b<0,a+b<0,将四个数a,b,﹣a,﹣b按由大到小的顺序排列是_____.(用“>”号连接)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把35°24′换算成度是_____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知线段AB∥x轴,端点A的坐标是(﹣1,4)且AB=4,则端点B的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个一元一次方程,同时满足方程的解为3,这个方程可以是_____.
相关试题

