【题目】(1)一个两位正整数,a表示十位上的数字,b表示个位上的数字(a≠b,ab≠0),则这个两位数用多项式表示为 (含a、b的式子);若把十位、个位上的数字互换位置得到一个新两位数,则这两个两位数的和一定能被 整除,这两个两位数的差一定能被 整除
(2)一个三位正整数F,各个数位上的数字互不相同且都不为0.若从它的百位、十位、个位上的数字中任意选择两个数字组成6个不同的两位数.若这6个两位数的和等于这个三位数本身,则称这样的三位数F为“友好数”,例如:132是“友好数”
一个三位正整数P,各个数位上的数字互不相同且都不为0,若它的十位数字等于百位数字与个位数字的和,则称这样的三位数P为“和平数”
①直接判断123是不是“友好数”?
②直接写出共有 个“和平数”
③通过列方程的方法求出既是“和平数”又是“友好数”的数.
参考答案:
【答案】(1) 10a+b,11,9;(2) ①123不是“友好数”,理由见解析;②32;③既是“和平数”又是“友好数”的数是396,264,132.
【解析】
(1)分别求出两数的和与两数的差即可得到结论;
(2)①根据“友好数”的定义判断即可;
②根据“和平数”的定义列举出所有的“和平数”即可;
③设三位数![]() 既是“和平数”又是“友好数”,根据“和平数”的定义,得出y=x+z.再由“友好数”的定义,得出10x+y+10y+x+10x+z+10z+x+10y+z+10z+y=100x+10y+z,化简即为12y=78x﹣21z.把y=x+z代入,整理得出z=2x,然后从②的数字中挑选出符合要求的数即可
既是“和平数”又是“友好数”,根据“和平数”的定义,得出y=x+z.再由“友好数”的定义,得出10x+y+10y+x+10x+z+10z+x+10y+z+10z+y=100x+10y+z,化简即为12y=78x﹣21z.把y=x+z代入,整理得出z=2x,然后从②的数字中挑选出符合要求的数即可
(1)这个两位数用多项式表示为10a+b,
(10a+b)+(10b+a)=10a+b+10b+a=11a+11b=11(a+b),
∵11(a+b)÷11=a+b(整数),
∴这个两位数的和一定能被数11整除;
(10a+b)﹣(10b+a)=10a+b﹣10b﹣a=9a﹣9b=9(a﹣b),
∵9(a﹣b)÷9=a﹣b(整数),
∴这两个两位数的差一定能被数9整除,
故答案为:11,9;
(2)①123不是“友好数”.理由如下:
∵12+21+13+31+23+32=132≠123,
∴123不是“友好数”;
②十位数字是9的“和平数”有198,297,396,495,594,693,792,891,一个8个;
十位数字是8的“和平数”有187,286,385,584,682,781,一个6个;
十位数字是7的“和平数”有176,275,374,473,572,671,一个6个;
十位数字是6的“和平数”有165,264,462,561,一个4个;
十位数字是5的“和平数”有154,253,352,451,一个4个;
十位数字是4的“和平数”有143,341,一个2个;
十位数字是3的“和平数”有132,231,一个2个;
所以,“和平数”一共有8+(6+4+2)×2=32个.
故答案为32;
③设三位数![]() 既是“和平数”又是“友好数”,
既是“和平数”又是“友好数”,
∵三位数![]() 是“和平数”,
是“和平数”,
∴y=x+z.
∵![]() 是“友好数”,
是“友好数”,
∴10x+y+10y+x+10x+z+10z+x+10y+z+10z+y=100x+10y+z,
∴22x+22y+22z=100x+10y+z,
∴12y=78x﹣21z.
把y=x+z代入,得12x+12z=78x﹣21z,
∴33z=66x,
∴z=2x,
由②可知,既是“和平数”又是“友好数”的数是396,264,132.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:为了求1+3+32+33+…+3100的值,可设M=1+3+32+33+…+3100,则3M=3+32+33+34+…+3101,因此3M﹣M=3101﹣1.所以M=
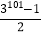 ,
,即1+3+32+33+…+3100=
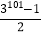 .问题解决:仿照上述方法求下列式子的值.
.问题解决:仿照上述方法求下列式子的值.(1)1+4+42+43+…+420.
(2)5101+5102+5103+…+52016.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是96分,请问小红在竞赛中答对了多少题?
(2)小明也参加了竞赛,考完后他说:“这次竟赛中我一定能拿到110分.”请问小明有没有可能拿到110分?试用方程的知识来说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
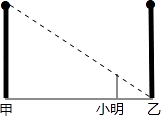
A.7米
B.8米
C.9米
D.10米 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋中,有若干个白色乒乓球和4个黄色乒乓球,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回袋中,通过大量重复摸球实验后发现,摸到黄球的频率稳定在40%,那么,估计袋中白色乒乓球的个数为( )
A.6
B.8
C.10
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
 与y=﹣kx+1(k≠0)在同一直角坐标系中的图象大致为( )
与y=﹣kx+1(k≠0)在同一直角坐标系中的图象大致为( )
A.
B.
C.
D.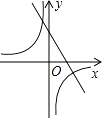
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组对该校学生一天的零用钱数额(单位:元)进行了随机抽样调查,现将抽样数据分成五组(第一组:0~1元,含0元,1元;第二组:1元~2元,含2元;第三组:2元~3元,含3元;第四组:3元~4元,含4元;第五组:4元~5元,含5元),其统计图如图所示.第一组的人数、频率分别为2,0.04,第二、三、五组的频率分别为0.24,0.20,0.36.

(1)该数学兴趣小组随机抽样了多少名学生?
(2)请你通过计算后,补全统计图.
(3)如果我们在校园中随机抽查一名学生,一天的零用钱在2元以上(不含2元)的学生被抽到的概率是多少?
相关试题

