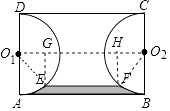
【题目】如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2 , 一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由 ![]() ,EF,
,EF, ![]() ,AB所围成图形(图中阴影部分)的面积等于 .
,AB所围成图形(图中阴影部分)的面积等于 . 
参考答案:
【答案】3﹣ ![]() ﹣
﹣ ![]()
【解析】解:连接O1O2 , O1E,O2F, 则四边形O1O2FE是等腰梯形,
过E作EG⊥O1O2 , 过F⊥O1O2 ,
∴四边形EGHF是矩形,
∴GH=EF=2,
∴O1G= ![]() ,
,
∵O1E=1,
∴GE= ![]() ,
,
∴ ![]() =
= ![]() ;
;
∴∠O1EG=30°,
∴∠AO1E=30°,
同理∠BO2F=30°,
∴阴影部分的面积=S ![]() ﹣2S
﹣2S ![]() ﹣S
﹣S ![]() =3×1﹣2×
=3×1﹣2× ![]() ﹣
﹣ ![]() (2+3)×
(2+3)× ![]() =3﹣
=3﹣ ![]() ﹣
﹣ ![]() .
.
所以答案是:3﹣ ![]() ﹣
﹣ ![]() .
.
【考点精析】本题主要考查了矩形的性质和扇形面积计算公式的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠DCE=118°,∠AEC的角平分线EF与GF相交于点F,∠BGF=132°,则∠F的度数是 .
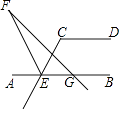
-
科目: 来源: 题型:
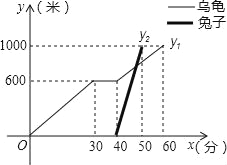
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了“龟免再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程),有下列说法:
①兔子和乌龟同时从起点出发;②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟; ④兔子比乌龟早10分钟到达终点.
其中正确的说法是_____(把你认为正确说法的序号都填上);
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运动品牌对第一季度A、B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图10所示:
(1)一月份B款运动鞋的销售量是A款的
 ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=﹣
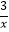 (x<0)与y=
(x<0)与y= 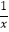 (x>0)的图象上,则ABCD的面积为 .
(x>0)的图象上,则ABCD的面积为 . 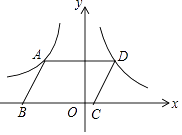
-
科目: 来源: 题型:
查看答案和解析>>【题目】水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
用户月用水量频数分布表
平均用水量(吨)
频数
频率
3~6吨
10
0.1
6~9吨
m
0.2
9~12吨
36
0.36
12~15吨
25
n
15~18吨
9
0.09

请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=__ __,n=__ __;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
-
科目: 来源: 题型:
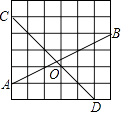
查看答案和解析>>【题目】在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .
相关试题

