【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2![]() ,则阴影部分图形的面积为( )
,则阴影部分图形的面积为( )
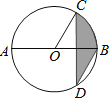
A.4π B.2π C.π D.![]()
参考答案:
【答案】D
【解析】
试题分析:根据垂径定理求得CE=ED=![]() ,然后由圆周角定理知∠COE=60°,然后通过解直角三角形求得线段OC、OE的长度,最后将相关线段的长度代入S阴影=S扇形OCB﹣S△COE+S△BED.
,然后由圆周角定理知∠COE=60°,然后通过解直角三角形求得线段OC、OE的长度,最后将相关线段的长度代入S阴影=S扇形OCB﹣S△COE+S△BED.
解:如图,假设线段CD、AB交于点E,
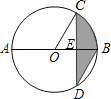
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=![]() ,
,
又∵∠CDB=30°,
∴∠COE=2∠CDB=60°,∠OCE=30°,
∴OE=CEcot60°=![]() ×
×![]() =1,OC=2OE=2,
=1,OC=2OE=2,
∴S阴影=S扇形OCB﹣S△COE+S△BED=![]() ﹣
﹣![]() OE×EC+
OE×EC+![]() BEED=
BEED=![]() ﹣
﹣![]() +
+![]() =
=![]() .
.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市今年预计建成34个地下调蓄设施,蓄水能力达到140000立方米,将140000用科学记数法表示应为( )
A.14×104 B.1.4×105 C.1.4×106 D.0.14×106
-
科目: 来源: 题型:
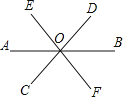
查看答案和解析>>【题目】如图直线AB、CD、EF相交于点O,是∠AOC的邻补角是 ,∠DOA的对顶角是 ,若∠AOC=50°,则∠BOD= 度,∠COB= 度.
-
科目: 来源: 题型:
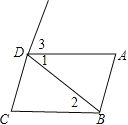
查看答案和解析>>【题目】推理填空:如图:
①若∠1=∠2,
则 ∥ (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 ∥ (同旁内角互补,两直线平行);
②当 ∥ 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 ∥ 时,
∠3=∠C (两直线平行,同位角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三条边距离相等的点是 ( )
A.三条角平分线的交点
B.三边中线的交点
C.三边上高所在直线的交点
D.三边的垂直平分线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC.
求证:∠1与∠2互余.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
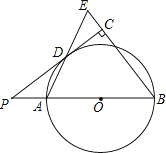
(1)求证:AB=BE;
(2)若PA=2,cosB=
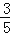 ,求⊙O半径的长.
,求⊙O半径的长.
相关试题

