【题目】如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.
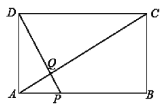
(1)求证:△APQ∽△CDQ;
(2)当PD⊥AC时,求线段PA的长度;
(3)当点P在线段AC的垂直平分线上时,
求sin∠ CPB的值.
参考答案:
【答案】(1)证明见解析;(2)PA=![]() ;(3)sin∠ CPB=
;(3)sin∠ CPB=![]() .
.
【解析】
试题分析:(1)利用两角对应相等的两个三角形易判断△APQ∽△CDQ;(2)由条件可推出△APD∽△DAC,得出![]() ,代入数值可求出PA的值;(3)由勾股定理能够求出PC的长度,再在Rt△CBP中求sin∠ CPB的值.
,代入数值可求出PA的值;(3)由勾股定理能够求出PC的长度,再在Rt△CBP中求sin∠ CPB的值.
试题解析:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠CAB=∠DCA,∠APQ=∠CDQ,∴△APQ∽△CDQ .
(2)PD⊥AC,∴∠ACD+∠PDC=90° ,∵∠PDA+∠PDA=90°,∴∠ACD=∠PDA,∵∠ADC=∠PAD=90°,∴△ADC∽△PDA,∴![]() ,
,![]() ,∴PA=
,∴PA=![]() .(3)当点P在线段AC的垂直平分线上时,PA=PC.设PA=x,则PB=10-x.又在矩形ABCD中,∠B=90°,∴
.(3)当点P在线段AC的垂直平分线上时,PA=PC.设PA=x,则PB=10-x.又在矩形ABCD中,∠B=90°,∴![]() ,∴
,∴![]() .解得:x=
.解得:x=![]() ,∴PC=PA=
,∴PC=PA=![]() .∴sin∠CPB=
.∴sin∠CPB=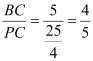
-
科目: 来源: 题型:
查看答案和解析>>【题目】气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( )
A.本市明天将有80%的地区降水
B.本市明天将有80%的时间降水
C.明天肯定下雨
D.明天降水的可能性比较大 -
科目: 来源: 题型:
查看答案和解析>>【题目】“建设大美青海,创建文明城市”,西宁市加快了郊区旧房拆迁的步伐.为了解被拆迁的236户家庭对拆迁补偿方案是否满意,小明利用周末调查了其中的50户家庭,有32户对方案表示满意.在这一抽样调查中,样本容量为
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市一月份某天的最高气温为零下5℃,最低气温为零下11℃,则当天气温的极差为 ℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数与反比例函数的图象相交于A(-4,-2),B(a,4)两点.
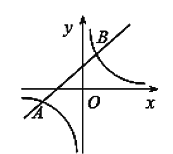
(1)求反比例函数的表达式和点B的坐标;
(2)根据图象直接同答:当白变量x在什么范围时,一次函数的值大于反比例函数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一盒乒乓球中共有6只,其中2只次品,4只正品,正品和次品大小和形状完全相同,每次任取3只,摸出至少有一只次品是 事件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题:若|a|=|b|,则 a2=b2,请写出该命题的逆命题______.
相关试题

