【题目】已知点D与点A(0,6),B(0,﹣4),C(x,y)是平行四边形的四个顶点,其中x,y满足x﹣y+3=0,则CD长的最小值为( )
A.![]()
B.4
C.2
D.2 ![]()
参考答案:
【答案】D
【解析】解:根据平行四边形的性质可知:对角线AB、CD互相平分,
∴CD过线段AB的中点M,即CM=DM,
∵A(0,6),B(0,﹣4),
∴M(0,1),
∵点到直线的距离垂线段最短,
∴过M作直线的垂线交直线于点C,此时CM最小,
直线x﹣y+3=0,令x=0得到y=3;令y=0得到x=﹣3,即F(﹣3,0),E(0,3),
∴OE=3,OF=3,EM=2,EF= ![]() =3
=3 ![]() ,
,
∵△EOF∽△ECM,
∴ ![]() ,
,
即 ![]() ,
,
解得:CM= ![]() ,
,
则CD的最小值为2CM=2 ![]() .
.
故选D.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:90°﹣53°17′=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼.有关成本、销售额见右表:

(1)2012年,王大爷养殖甲鱼20亩,桂鱼10亩.求王大爷这一年共收益多少万元?(收益=销售额-成本)
(2)2013年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元.若每亩养殖的成本、销售额与2012年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
(3)已知甲鱼每亩需要饲料500kg,桂鱼每亩需要饲料700kg.根据(2)中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需全部饲料比原计划减少了2次.求王大爷原定的运输车辆每次可装载饲料多少kg?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于有理数a、b,定义a*b=3a+2b,化简x*(x﹣y)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
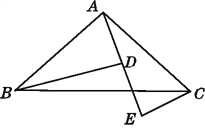
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
-
科目: 来源: 题型:
查看答案和解析>>【题目】空气的平均密度为0.00124g/cm3,用科学记数法表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=
 ,其中正确的有( )
,其中正确的有( ) 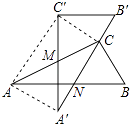
A.2个
B.3个
C.4个
D.5个
相关试题

