【题目】如图,在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象经过点
的图象经过点![]() ,且当
,且当![]() 和
和![]() 时所对应的函数值相等.一次函数
时所对应的函数值相等.一次函数![]() 与二次函数
与二次函数![]() 的图象分别交于
的图象分别交于![]() ,
, ![]() 两点,点
两点,点![]() 在第一象限.
在第一象限.

(![]() )求二次函数
)求二次函数![]() 的表达式.
的表达式.
(![]() )连接
)连接![]() ,求
,求![]() 的长.
的长.
(![]() )连接
)连接![]() ,
, ![]() 是线段
是线段![]() 得中点,将点
得中点,将点![]() 绕点
绕点![]() 旋转
旋转![]() 得到点
得到点![]() ,连接
,连接![]() ,
, ![]() ,判断四边形
,判断四边形![]() 的性状,并证明你的结论.
的性状,并证明你的结论.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】(1)根据当x=0和x=5时所对应的函数值相等,可得(5,c),根据待定系数法,可得函数解析式;
(2)联立抛物线与直线,可得方程组,根据解方程组,可得B、C 的坐标根据勾股定理,可得AB的长;
(3)根据线段中点的性质,可得M点的坐标,根据旋转的性质,可得MN与BM的关系,根据平行四边形的判定,可得答案.
解:(![]() )当
)当![]() 时
时![]() .即
.即![]() .
.
把![]()
![]() 代入解析式.
代入解析式.
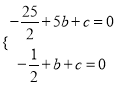 ,∴
,∴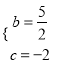 ,
,
∴![]() .
.
(![]() )∵
)∵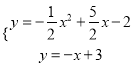 ,∴
,∴![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
,
∴![]() .
.
(![]() )四边形
)四边形![]() 为矩形.
为矩形.
证:∵![]() 为
为![]() 中点,∴
中点,∴![]() .
.
又∵![]() ,∴四边形
,∴四边形![]() 为平行四边形.
为平行四边形.
又∵,∴
![]() .
.
在![]() 中.
中.
![]() .
.
∴![]() ,
,
∴四边形![]() 为矩形.
为矩形.
“点睛”本题考查了二次函数综合题,利用函数值相等得出(5,c)是解题关键,又利用了待定系数法求函数解析式;利用解方程组得出交点坐标,又利用了勾股定理;利用了平行四边形的判定;对角线互相平分的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下面各组线段的长为边,能组成三角形的是( )
A. 1、2、3 B. 3、4、8 C. 5、6、11 D. 2、3、4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图象的对称轴是直线
的图象的对称轴是直线 ,则下列理论:①
,则下列理论:① ,
,  ②
② ,③
,③ ,④
,④ ,⑤当
,⑤当 时,
时,  随
随 的增大而减小,其中正确的是( ).
的增大而减小,其中正确的是( ).
A. ①②③ B. ②③④ C. ③④⑤ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a与1互为相反数,则|a+1|等于( )
A.-1
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 与
与 分别是两个函数图象
分别是两个函数图象 与
与 上的任一点.当
上的任一点.当 时,有
时,有 成立,则称这两个函数在
成立,则称这两个函数在 上是“相邻函数”,否则称它们在
上是“相邻函数”,否则称它们在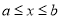 上是“非相邻函数”.例如,点
上是“非相邻函数”.例如,点 与
与 分别是两个函数
分别是两个函数 与
与 图象上的任一点,当
图象上的任一点,当 时,
时,  ,通过构造函数
,通过构造函数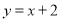 并研究它在
并研究它在 上的性质,得到该函数值得范围是
上的性质,得到该函数值得范围是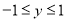 ,所以
,所以 成立,因此这两个函数在
成立,因此这两个函数在 上是“相邻函数”.
上是“相邻函数”.(
 )判断函数
)判断函数 与
与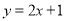 在
在 上是否为“相邻函数”,并说明理由.
上是否为“相邻函数”,并说明理由.(
 )若函数
)若函数 与
与 在
在 上是“相邻函数”,求
上是“相邻函数”,求 的取值范围.
的取值范围.(
 )若函数
)若函数 与
与 在
在 上是“相邻函数”,直接写出
上是“相邻函数”,直接写出 的最大值与最小值.
的最大值与最小值.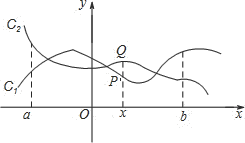
-
科目: 来源: 题型:
查看答案和解析>>【题目】25的平方根等于( )
A.5B.-25C.±25D.±5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边长分别为3cm,5cm,设第三边为xcm,则x的取值范围是 .
相关试题

