【题目】如图,在Rt△ABC中,∠C=90°,sinA= ![]() ,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.
,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF. 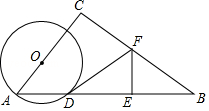
(1)求证:DF为⊙O的切线;
(2)若AO=x,DF=y,求y与x之间的函数关系式.
参考答案:
【答案】
(1)证明:连接OD.
∵OA=OD,
∴∠OAD=∠ODA,
∵EF是BD的中垂线,
∴DF=BF.
∴∠FDB=∠B,
∵∠C=90°,
∴∠OAD+∠B=90°.
∴∠ODA+∠FDB=90°.
∴∠ODF=90°,
又∵OD为⊙O的半径,
∴DF为⊙O的切线
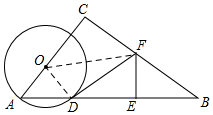
(2)解:连接OF.
在Rt△ABC中,
∵∠C=90°,sinA= ![]() ,AB=10,
,AB=10,
∴AC=6,BC=8,
∵AO=x,DF=y,
∴OC=6﹣x,CF=8﹣y,
在Rt△COF中,
OF2=(6﹣x)2+(8﹣x)2
在Rt△ODF中,
OF2=x2+y2
∴(6﹣x)2+(8﹣x)2=x2+y2,
∴y=﹣ ![]() x+
x+ ![]() (0<x≤6)
(0<x≤6)

【解析】(1)连接OD,由于EF是BD的中垂线,DF=BF.从而可知∠FDB=∠B,又因为OA=OD,所以∠OAD=∠ODA,从而可证明∠ODF=90°;(2)连接OF,由题意可知:AO=x,DF=y,OC=6﹣x,CF=8﹣y,然后在Rt△COF中与Rt△ODF中利用勾股定理分别求出OF,化简原式即可求出答案.
【考点精析】利用线段垂直平分线的性质和解直角三角形对题目进行判断即可得到答案,需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点
票价
历史博物馆
10元/人
民俗展览馆
20元/人
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一次函数
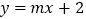 的图象经过点
的图象经过点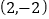 .
.(1)求m的值;
(2)画出此函数的图象;
(3)平移此函数的图象,使得它与两坐标轴所围成的图形的面积为4,请直接写出此时图象所对应的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣
 x2+
x2+  x+4经过A、B两点.
x+4经过A、B两点.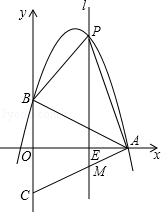
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为( )
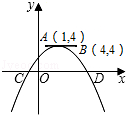
A.﹣3
B.1
C.5
D.8 -
科目: 来源: 题型:
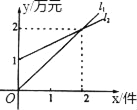
查看答案和解析>>【题目】如图,l1表示某公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.
(1)x=1时,销售收入= 万元,销售成本= 万元,盈利(收入﹣成本)= 万元;
(2)一天销售 件时,销售收入等于销售成本;
(3)l2对应的函数表达式是 ;
(4)你能写出利润与销售量间的函数表达式吗?
相关试题

