【题目】已知二次函数![]() 的图象与y轴交于点C(0,﹣6),与x轴的一个交点坐标是A(﹣2,0).
的图象与y轴交于点C(0,﹣6),与x轴的一个交点坐标是A(﹣2,0).
(1)求二次函数的解析式,并写出顶点D的坐标;
(2)将二次函数的图象沿x轴向左平移![]() 个单位长度,当 y<0时,求x的取值范围.
个单位长度,当 y<0时,求x的取值范围.

参考答案:
【答案】(1)![]() ,D(
,D(![]() ,
,![]() );(2)
);(2)![]() <x<
<x<![]() .
.
【解析】
试题分析:(1)将点A和点C的坐标代入抛物线的解析式可求得b、c的值,从而得到抛物线的解析式,然后依据配方法可求得抛物线的顶点坐标;
(2)依据抛物线的解析式与平移的规划规律,写出平移后抛物线的解析式,然后求得抛物线与x轴的交点坐标,最后依据y<0可求得x的取值范围.
试题解析:(1)∵把C(0,﹣6)代入抛物线的解析式得:C=﹣6,把A(﹣2,0)代入![]() 得:b=﹣1,∴抛物线的解析式为
得:b=﹣1,∴抛物线的解析式为![]() ,∴
,∴![]() ,∴抛物线的顶点坐标D(
,∴抛物线的顶点坐标D(![]() ,
,![]() ).
).
(2)二次函数的图形沿x轴向左平移![]() 个单位长度得:
个单位长度得:![]() .令y=0得:
.令y=0得:![]() ,解得:
,解得:![]() ,
,![]() .∵a>0,∴当y<0时,x的取值范围是
.∵a>0,∴当y<0时,x的取值范围是![]() <x<
<x<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:25﹣a2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算的结果是x5的为( )
A.x10÷x2B.x6﹣xC.x2x3D.(x2)3
-
科目: 来源: 题型:
查看答案和解析>>【题目】小文,小亮从学校出发到青少年宫参加书法比赛,小文步行一时间后,小亮骑自行车沿相同路线行走,两人均匀速前行,他们的路程差s(米)与小文出发时间t(分)之间的关系如图所示.
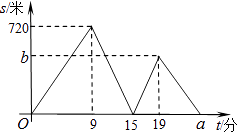
(1)求小文和小亮的速度各是多少?
(2)求学校到少年宫的距离.
(3)求图中的a,b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】多项式3x2-12与多项式x2-4x+4的公因式是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( )
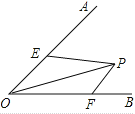
A. 30° B. 45° C. 60° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠1与∠2是同位角,则它们之间的关系是( ).
A. ∠1=∠2 ; B. ∠1>∠2 ;
C. ∠1<∠2; D. ∠1=∠2或∠1>∠2或∠1<∠2.
相关试题

