Question

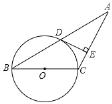
【题目】如图，在△ABC中，∠A=30°，AC=BC，以BC为直径的⊙O与边AB交于点D，过D作DE⊥AC于E．

（1）证明：DE为⊙O的切线．

（2）若⊙O的半径为2，求AD的长．

Answer 1

【答案】(1)见解析;(2)2.

【解析】

（1）连接OD，根据等腰三角形的性质、平行线的判定定理得到OD∥AC，得到DE⊥OD，根据切线的判定定理证明；（2）连接DC，根据圆周角定理、正弦的定义计算即可．

（1）证明：连接OD，

∵OB=OD，

∴∠ODB=∠B，

∵CA=CB，

∴∠A=∠B，

∴∠ODB=∠A，

∴OD∥AC，

∵DE⊥AC，

∴DE⊥OD，

∴DE为⊙O的切线；

（2）解：连接DC，

∵⊙O的半径为2，

∴CA=CB=4，

∵BC为⊙O的直径，

∴∠BDC=90°，

在Rt△ADC中，AD=ACcosA=2．