【题目】对于实数a,我们规定:用符号![]() 表示不大于
表示不大于![]() 的最大整数,称
的最大整数,称![]() 为a的根整数,例如:
为a的根整数,例如: ![]() ,
, ![]() .
.
(1)仿照以上方法计算: ![]() = ;
= ; ![]() = .
= .
(2)若![]() =1,写出满足题意的x的整数值 .
=1,写出满足题意的x的整数值 .
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 ![]() ,这时候结果为1.
,这时候结果为1.
(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
参考答案:
【答案】(1) 2,5;(2) 1,2,3;(3)3;(4)255.
【解析】试题分析:
(1)由![]() ,
, ![]() 结合根整数的定义即可得到结果;
结合根整数的定义即可得到结果;
(2)由![]() 结合
结合![]() 可得x=1或2或3;
可得x=1或2或3;
(3)按题意对100连续求根整数至到结果为1即可得到所求答案;
(4)由![]() 结合22=4,42=16,162=256可知256是所有正整数中需连续进行4次求根整数的运算才能使结果为1的正整数中最小的一个,由此可知255是所有正整数中需连续经过3次求根整数运算才能使结果为1的正整数中最大的1个.
结合22=4,42=16,162=256可知256是所有正整数中需连续进行4次求根整数的运算才能使结果为1的正整数中最小的一个,由此可知255是所有正整数中需连续经过3次求根整数运算才能使结果为1的正整数中最大的1个.
试题解析:
(1)∵22=4,52=25,62=36,
∴5<![]() <6,
<6,
∴![]() =[2]=2,[
=[2]=2,[![]() ]=5,
]=5,
故答案为:2,5;
(2)∵12=1,22=4,且![]() ,
,
∴x=1,2,3,
故答案为:1,2,3;
(3)第一次:[![]() ]=10,
]=10,
第二次:[![]() ]=3,
]=3,
第三次:[![]() ]=1,
]=1,
故答案为:3;
(4)最大的正整数是255,理由如下:
∵[![]() ]=15,[
]=15,[![]() ]=3,[
]=3,[![]() ]=1,
]=1,
∴对255只需进行3次操作后变为1,
∵[![]() ]=16,[
]=16,[![]() ]=4,[
]=4,[![]() ]=2,[
]=2,[![]() ]=1,
]=1,
∴对256需进行4次操作后才能变为1,
∴只需进行3次操作后变为1的所有正整数中,最大的是255,
故答案为:255.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)求证:AB∥CD;
(2)如图2,∠AEF与∠EFC的角平分线相交于点P,直线EP与直线CD交于点G,过点G做EG的垂线,交直线MN于点H.求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点,且∠PHK=∠HPK,作∠EPK的平分线交直线MN于点Q.问∠HPQ的大小是否发生变化?若不变,请求出∠HPQ的度数;若变化,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a,我们规定:用符号
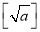 表示不大于
表示不大于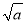 的最大整数,称
的最大整数,称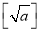 为a的根整数,例如:
为a的根整数,例如: 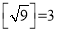 ,
, 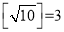 .
.(1)仿照以上方法计算:
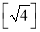 = ;
= ; 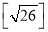 = .
= .(2)若
 =1,写出满足题意的x的整数值 .
=1,写出满足题意的x的整数值 .如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次
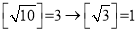 ,这时候结果为1.
,这时候结果为1.(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度上升-3后,又下降2实际上就是 ( )
A. 上升1 B. 上升5 C.下降5 D. 下降-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:8x-1=2x-7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;…;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.
(1)如图1,矩形ABCD中,若AB=3,BC=9,则称矩形ABCD为 阶奇异矩形.
(2)如图2,矩形ABCD长为7,宽为3,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(3)已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方直接写出a的值.

相关试题

