Question

【题目】如下图1,在四边形ABCD中，点E、F分别是AB、CD的中点.过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连结GA、GB、GC、GD、EF,若∠AGD=∠BGC.

（1）求证:AD=BC；

（2）求证:△AGD∽△EGF；

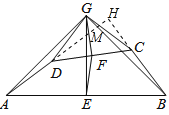
（3）如图2,若AD、BC所在直线互相垂直,求的值.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）.

【解析】

试题分析：本题是相似形综合题目，考查了线段垂直平分线的性质、全等三角形的判定与性质、相似三角形的判定与性质、三角函数等知识；本题难度较大，综合性强，特别是（3）中，需要通过作辅助线综合运用（1）（2）的结论和三角函数才能得出结果.

（2）先证出∠AGB=∠DGC，由=，证出△AGB∽△DGC，得出比例式=，再证出∠AGD=∠EGF，即可得出△AGD∽△EGF；

（3）延长AD交GB于点M，交BC的延长线于点H，则AH⊥BH，由△AGD≌△BGC，得出∠GAD=∠GBC，再求出∠AGE=∠AHB=90°，得出∠AGE=∠AGB=45°，求出=，由△AGD∽△EGF，即可得出的值即可.

试题解析：（1）∵GE是AB的垂直平分线，

∴GA=GB，

同理：GD=GC，

在△AGD和△BGC中，

，

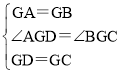∴△AGD≌△BGC（SAS），

∴AD=BC；

（2）∵∠AGD=∠BGC，

∴∠AGB=∠DGC，

在△AGB和△DGC中，=，

∴△AGB∽△DGC，

∴=，

又∵∠AGE=∠DGF，

∴∠AGD=∠EGF，

∴△AGD∽△EGF；

（3）延长AD交GB于点M，交BC的延长线于点H，如图所示，则AH⊥BH，

∵△AGD≌△BGC，

∴∠GAD=∠GBC，

在△GAM和△HBM中，∠GAD=∠GBC，∠GMA=∠HMB，

∴∠AGB=∠AHB=90°，

∴∠AGE=∠AGB=45°，

∴=，

又∵△AGD∽△EGF，

∴==.