【题目】抛物线y=x2+2x+m与x轴有两个不同的交点,求m的取值范围.
参考答案:
【答案】m<1.
【解析】
抛物线与x轴有两个交点,则△=b2-4ac>0,从而求出m的取值范围.
∵抛物线y=x2+2x+m与x轴有两个不同交点,
∴△=4-4m>0,
解得m<1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.
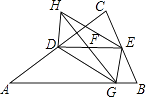
(1)求证:四边形HDGE是平行四边形.
(2)已知∠C=90°,∠A=30°,AB=4.
①当AG为何值时,四边形HDGE是矩形;
②当AG为何值时,四边形HDGE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式x+3≤6的正整数解为___________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,﹣2,0,1四个数中最小的数是( )
A.﹣1
B.﹣2
C.0
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=10,对角线AC=12.若过点A作AE⊥CD,垂足为E,则AE的长为( )
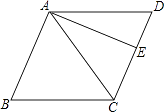
A.9
B.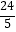
C.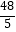
D.9.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数的图像在每一个象限内,
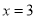 值随
值随 值的增大而增大的是( )
值的增大而增大的是( )A.
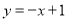 B.
B. 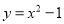 C.
C.  D.
D. 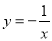
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4a﹣ab2= .
相关试题

