【题目】如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c过A,B两点,且与x轴交于另一点C.
(1)求b、c的值;
(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;
(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内一点,连接PA,PC,PG,分别以AP,AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR
①求证:PG=RQ;
②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.
参考答案:
【答案】
(1)
解:∵一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,
∴A(﹣3,0),B(0,3),
∵抛物线y=﹣x2+bx+c过A、B两点,
∴ ![]() 解得
解得 ![]() ,
,
∴b=﹣2,c=3
(2)
解:对于抛物线y=﹣x2﹣2x+3,令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,
∴点C坐标(1,0),
∵AD=DC=2,
∴点D坐标(﹣1,0),
∵BE=2ED,
∴点E坐标(﹣ ![]() ,1),
,1),
设直线CE为y=kx+b,把E、C代入得到  解得
解得  ,
,
∴直线CE为y=﹣ ![]() x+
x+ ![]() ,
,
由  解得
解得 ![]() 或
或  ,
,
∴点M坐标(﹣ ![]() ,
, ![]() )
)
(3)
解:①证明:∵△AGQ,△APR是等边三角形,
∴AP=AR,AQ=AG,∠QAC=∠RAP=60°,
∴∠QAR=∠GAP,
在△QAR和△GAP中,
 ,
,
∴△QAR≌△GAP,
∴QR=PG.
②如图3中,∵PA+PB+PC=QR+PR+PC=QC,
∴当Q、R、P、C共线时,PA+PG+PC最小,
作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K.
∵∠GAO=60°,AO=3,
∴AG=QG=AQ=6,∠AGO=30°,
∵∠QGA=60°,
∴∠QGO=90°,
∴点Q坐标(﹣6,3 ![]() ),
),
在RT△QCN中,QN=3 ![]() ,CN=7,∠QNC=90°,
,CN=7,∠QNC=90°,
∴QC= ![]() =2
=2 ![]() ,
,
∵sin∠ACM= ![]() =
= ![]() ,
,
∴AM= ![]() ,
,
∵△APR是等边三角形,
∴∠APM=60°,∵PM=PR,cos30°= ![]() ,
,
∴AP= ![]() ,PM=RM=
,PM=RM= ![]()
∴MC= ![]() =
= ![]() ,
,
∴PC=CM﹣PM= ![]() ,
,
∵ ![]() =
= ![]() =
= ![]() ,
,
∴CK= ![]() ,PK=
,PK= ![]() ,
,
∴OK=CK﹣CO= ![]() ,
,
∴点P坐标(﹣ ![]() ,
, ![]() ).
).
∴PA+PC+PG的最小值为2 ![]() ,此时点P的坐标(﹣
,此时点P的坐标(﹣ ![]() ,
, ![]() ).
).

【解析】(1)把A(﹣3,0),B(0,3)代入抛物线y=﹣x2+bx+c即可解决问题.(2)首先求出A、C、D坐标,根据BE=2ED,求出点E坐标,求出直线CE,利用方程组求交点坐标M.(3)①欲证明PG=QR,只要证明△QAR≌△GAP即可.②当Q、R、P、C共线时,PA+PG+PC最小,作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K,由sin∠ACM= ![]() =
= ![]() 求出AM,CM,利用等边三角形性质求出AP、PM、PC,由此即可解决问题.
求出AM,CM,利用等边三角形性质求出AP、PM、PC,由此即可解决问题.
【考点精析】关于本题考查的一次函数的概念和一次函数的图象和性质,需要了解一般地,如果y=kx+b(k,b是常数,k不等于0),那么y叫做x的一次函数;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于
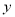 轴对称的
轴对称的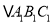 ,并写出
,并写出 三个顶点的坐标:
三个顶点的坐标: 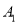 ( ),
( ),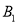 ( ),
( ), ( );
( );(2)直接写出△ABC的面积为 ;
(3)在
 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.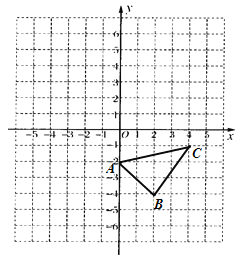
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3 ,求AG,MN的长.
,求AG,MN的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E、F分别在边BC,CD上,且BE=DF,点P是AF的中点,点Q是直线AC与EF的交点,连接PQ,PD.
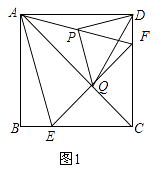
(1)求证:AC垂直平分EF;
(2)试判断△PDQ的形状,并加以证明;
(3)如图2,若将△CEF绕着点C旋转180°,其余条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.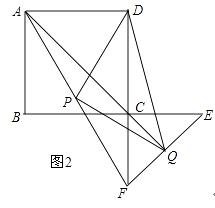
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中, 于E,
于E, ,D是AE上的一点,且
,D是AE上的一点,且 ,连接BD,CD.
,连接BD,CD.
 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由; 如图2,若将
如图2,若将 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由; 如图3,若将
如图3,若将 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变. 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论; 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
相关试题

