【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与 CD1交于点O,则线段AD1的长为( ) 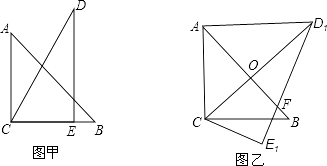
A.6 ![]()
B.10
C.8
D.![]()
参考答案:
【答案】B
【解析】解:∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°﹣30°=60°,
∴∠ACD=90°﹣60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°,
又∵∠A=45°,
∴△ACO是等腰直角三角形,
∴AO=CO= ![]() AB=
AB= ![]() ×12=6,AB⊥CO,
×12=6,AB⊥CO,
∵DC=14,
∴D1C=DC=14,
∴D1O=14﹣6=8,
在Rt△AOD1中,AD1= ![]() =
= ![]() =10.
=10.
故选:B.
先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°,然后判断出△ACO是等腰直角三角形,再根据等腰直角三角形的性质求出AO、CO,AB⊥CO,再求出OD1然后利用勾股定理列式计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=
 ,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)= .
.(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1.
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某巡警骑摩托车在一条南北大道上来回巡逻,一天早晨,他从岗亭出发,中午停留在
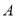 处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:千米):+5,﹣4,+3,﹣7,+4,﹣8,+2,﹣1.
处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:千米):+5,﹣4,+3,﹣7,+4,﹣8,+2,﹣1.(1)
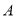 处在岗亭何方?距离岗亭多远?
处在岗亭何方?距离岗亭多远?(2)若摩托车每行驶1千米耗油
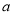 升,这一天上午共耗油多少升?
升,这一天上午共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N,
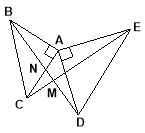
证明:(1)BD=CE. (2)BD⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产一批零件,根据要求,圆柱体的内径可以有0.03毫米的误差,抽查5个零件,超过规定内径的记作正数,不足的记作负数,检查结果如下:+0.025,﹣0.035,+0.016,﹣0.010,+0.041
(1)指出哪些产品合乎要求?
(2)指出合乎要求的产品中哪个质量好一些?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某巡警车在一条南北大道上巡逻,某天巡警车从岗亭
 处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)﹣10,﹣9,+7,﹣15,+6,﹣5,+4,﹣2
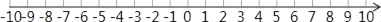
(1)最终巡警车是否回到岗亭
 处?若没有,在岗亭何方,距岗亭多远?
处?若没有,在岗亭何方,距岗亭多远?(2)摩托车行驶1千米耗油0.2升,油箱有油10升,够不够?若不够,途中还需补充多少升油?
相关试题

