【题目】如图,两块大小不等的等腰直角三角形按图1放置,点![]() 为直角顶点,点
为直角顶点,点![]() 在
在![]() 上,将
上,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角度
角度![]() ,连接
,连接![]() 、
、![]() .
.
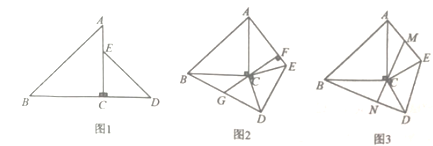
(1)若![]() ,则当
,则当![]()
![]() 时,四边形
时,四边形![]() 是平行四边形;
是平行四边形;
(2)图2,若![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() 是
是![]() 的中点;
的中点;
(3)图3,若点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)![]() 时,四边形
时,四边形![]() 是平行四边形;(2)见解析;(3)见解析.
是平行四边形;(2)见解析;(3)见解析.
【解析】
(1)当AC∥DE时,因为AC=DE,推出四边形ACDE是平行四边形,利用平行四边形的性质即可解决问题.
(2)如图2中,作DM⊥FM于M,BN⊥FM交FM的延长线于N.利用全等三角形的性质证明BN=DM,再证明△BNG≌△DMG(AAS)即可解决问题.
(3)如图3中,延长CM到K,使得MK=CM,连接AK.KM.想办法证明△BCD≌△CAK(SAS),即可解决问题.
(1)解:如图1-1中,连接AE.
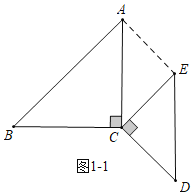
当AC∥DE时,∵AC=DE,
∴四边形ACDE是平行四边形,
∴∠ACE=∠CED,
∵CE=CD,∠ECD=90°,
∴∠CED=45°,
∴α=∠ACE=45°.
故答案为45.
(2)证明:如图2中,作DM⊥FM于M,BN⊥FM交FM的延长线于N.
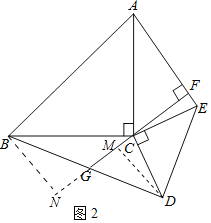
∵CF⊥AE,DM⊥FM,
∴∠CFE=∠CMD=∠ECD=90°,
∴∠ECF+∠CEF=90°,∠ECF+∠DCM=90°,
∴∠CEF=∠DCM,∵CE=CD,
∴△CFE≌△DMC(AAS),
∴DM=CF,
同法可证:CF=BN,
∴BN=DM,
∵BN⊥FM,
∴∠N=∠DMG=90°,
∵∠BGN=∠DGM,
∴△BNG≌△DMG(AAS),
∴BG=DG,
∴点G是BD的中点.
(3)证明:如图3中,延长CM到K,使得MK=CM,连接AK.KM.
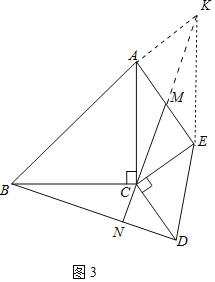
∵AM-ME,CM=MK,
∴四边形ACEK是平行四边形,
∴AK=CE=CD,AK∥CE,
∴∠KAC+∠ACE=180°,
∵∠ACE+∠BCD=180°,
∴∠BCD=∠KAC,
∵CA=CB,CD=AK,
∴△BCD≌△CAK(SAS),
∵∠ACK=∠CBD,
∵∠ACK+∠BCN=90°,
∴∠CBD+∠BCN=90°,
∴∠CNB=90°,
∴CN⊥BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
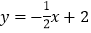 与双曲线
与双曲线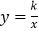 相交于点A(m,3),与x轴交于点C.
相交于点A(m,3),与x轴交于点C.(1)求双曲线的解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区. 已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知拋物线
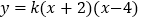 (k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线
(k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线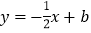 与抛物线的另一个交点为D.
与抛物线的另一个交点为D.(1)若点D的横坐标为x= -4,求这个一次函数与抛物线的解析式;
(2)若直线m平行于该抛物线的对称轴,并且可以在线段AB间左右移动,它与直线BD和抛物线分别交于点E、F,求当m移动到什么位置时,EF的值最大,最大值是多少?
(3)问原抛物线在第一象限是否存在点P,使得△APB∽△ABC?若存在,请求出这时k的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣6,点B表示10,点C表示14,我们称点A和点C在数轴上相距20个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
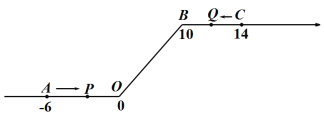
问:
(1)动点P从点A运动至C点需要时间为 秒;P、Q两点相遇时,求出相遇点M所对应的数是 ;
(2)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. “清明时节雨纷纷”是必然事件
B. 了解路边行人边步行边低头看手机的情况可以采取对在路边行走的学生随机发放问卷的方式进行调查
C. 射击运动员甲、乙分别射击10次且击中环数的方差分别是0.5和1.2,则甲队员的成绩好
D. 分别写有三个数字 -1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
相关试题

